Ian Short

Introduction

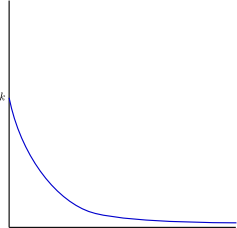
Last week E asked me about some biological data which could be modelled by an exponential curve, similar to the one shown below. It is the graph of a function such as f(x) = kexp(-sx), for positive constants k and s.

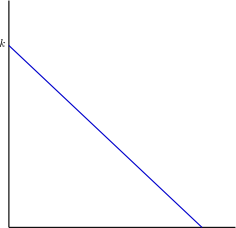
Ellie had another version of this graph, shown below.

I immediately thought that this was the graph of log f, rather than f, and that the intercept with the vertical axis should be at log k, rather than k. However, E said that this graph was a semi-log graph, and I later realised what she meant by this, and that the intercept with the vertical axis should indeed be k rather than log k.

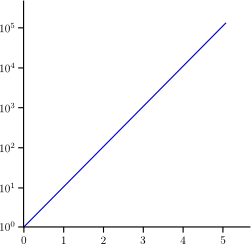
To give you an idea of what a semi-log graph is, here is an example of such a graph, with the axes labels carefully marked. This semi-log graph uses log to base 10, rather than log to base e.

On the vertical axis, the label b occurs where the label log b would usually occur. The horizontal axis remains as usual. Hence the phrase semi-log. Adjusting the scale of the vertical axis affects the graph (and likewise for the horizontal axis). A question presents itself: how much freedom do we have in changing the shape of a graph by adjusting the horizontal and vertical axes? I thought this question might lead to a source of problems for NRICH.

Examples

From now on, for simplicity, we restrict attention to maps that fix 0. In the next diagram, the graph of the function f(x)=x is altered by a change in the vertical axis scale.

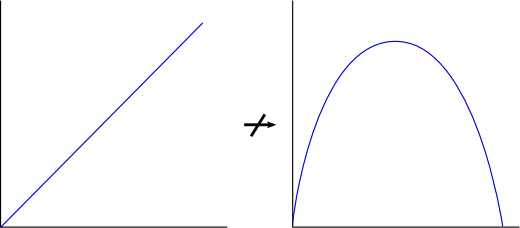
We are allowed to expand and contract the vertical axis scale as we wish, but the ordering of the axis labels must remain the same if the graph is to be of any use at all. With this freedom, f(x)=x can be transformed to g(x)=x³ and h(x)=e^x-1. It is impossible to create from f(x)=x a graph with a stationary point though, as indicated in the next diagram.

The reason for this will be explained later. Likewise the two graphs in the next diagram cannot be transformed from one to the other.

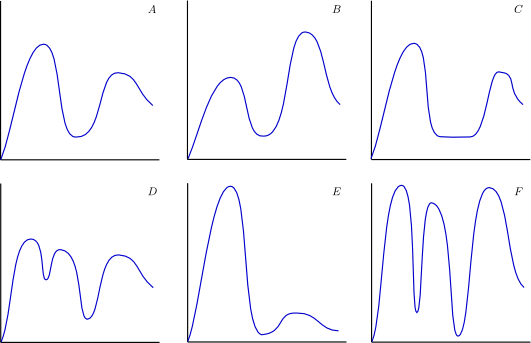
The left hand graph has a maximum, followed by a minimum, and then another maximum. The right hand graph has a maximum, followed by a minimum, and then a saddle point. That means these two graphs are inequivalent. Here is another set of examples.

Graph A is not equivalent to graph B because the first maximum of A is larger than the second maximum of A, whereas the first maximum of B is smaller than the second maximum of B. Graph A is not equivalent to graph C because graph C has a whole interval of stationary points. Graph A is not equivalent to graph D because graph D has five stationary points, whereas graph A has only three. Graph A is equivalent to graph E: they both have three stationary points, and each function takes its maximum value at the first stationary point, and its minimum value at the second stationary point. Graph A is not equivalent to graph F because graph F has five stationary points. Graph F is not equivalent to graph D because the ordering of the values of the functions at the stationary points differ. In fact, of the six graphs, only graphs A and E are equivalent.

In the next two sections we study our problem formally.

Graph equivalence

In this formal explanation we restrict attention to the class U of continuously differentiable real functions which map [0,∞) to itself, and which fix the point 0. In this class we can explain the key ideas, and it is easy to generalise to include all the functions shown above.

The graph G(f) of an element of U is the set {(x,f(x)) : x>0}. The semi-log graph of f is the graph G(log f), but with the label b on the vertical axis replaced with exp b. However, log f is not a member of U, so we introduce another class V consisting of strictly increasing continuously differentiable maps of [0,∞) onto itself. Contracting and expanding the vertical axis of the graph of f is equivalent to replacing G(f) with G(gf), where g is a member of V. Likewise, contracting and expanding the horizontal axis of f is equivalent to replacing G(f) with G(fh), where, again, h is a member of V. We ignore issues about labelling of the horizontal and vertical axes as they are a distraction. Let us say that two elements f₁ and f₂ of U are equivalent if there exist maps g and h in V such that f₂= gf₁h. This is an equivalence relation on U. The question from the end of the first section becomes:

what are the equivalence classes of U?

Or, in other words:

given maps f₁ and f₂ in U, do there exist maps g and h in V such that f₂ = gf₁h?

Stationary points

Suppose that f₁ and f₂ are equivalent elements in U, with f₂ = gf₁h. What common features do they have? Suppose that f₁‘(x)=0. Then, by the chain-rule, f₂‘(x)=0 also. This means that f₁ and f₂ must have the same number of critical points. For simplicity, let us restrict to the subset W of U consisting of those elements f of U which have finitely many critical points, and are such that if a and b are critical points of f, then f(a) and f(b) are distinct.

Let f have critical points p₁ < p₂ < … < p_n, and let q₁, q₂,…,q_n be the corresponding critical values (so that q_i=f(p_i)). Let γ denote the unique permutation from S_n such that q_γ(1) < q_γ(2) < … < q_γ(n). We describe γ as the permutation associated to f. The following theorem characterises equivalence in terms of permutations.

Theorem.Two elements of W are equivalent if and only if their associated permutations are equal.

Sketch proof. Suppose first that f₁ and f₂ are equivalent elements in U, which means that there are maps g and h in V such that f₂ = gf₁h^-1. Let p₁ < p₂ < … < p_n be the critical points of f₁, and let γ be the permutation associated to f. Then the critical points of f₂ are h(p₁) < h(p₂) < … < h(p_n), and the critical values are f₂h(p_i) for i=1,2,…,n. However, f₂h = gf₁, which means that the critical values of f₂ are gf₁(p_i) for i=1,2,…,n. Since g preserves order, the permutation associated to f₂ is also γ.

Conversely, if the permutations associated to f₁ and f₂ are equal then, after applying preliminary transformations on the left and right, we can assume that they have identical critical points and critical values. That is, we can assume that f₁ and f₂ both have critical points p₁ < p₂ < … < p_n, and critical values q₁, q₂,…,q_n. To finish the proof, define p₀=0, p_n+1=∞, and define h to be the element of U that is equal to f₂^-1f₁ when restricted to the interval [p_i-1,p_i], for i=1,2,…,n+1. Then f₂h = f₁, and this completes the proof.

There is a similar (but slightly more complicated) theorem for U rather than W.