Graph theory and game theory
by Ian Short
Some months ago I discussed the following problem with Steve Hewson and Mike Pearson after an NRICH meeting. Two people play a game with a finite graph. They take turns in colouring the uncoloured vertices of the graph, one vertex at a time. One player colours vertices red, and the other player colours vertices green. Two adjacent vertices (vertices joined by an edge) cannot be coloured in the same way. The loser of the game is the first person who is unable to colour a vertex.
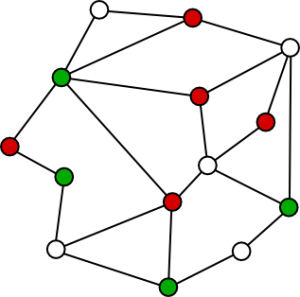
Figure 1. Green is unable to colour a vertex.
The optimal strategy for each player depends on the graph. For a graph with no edges, player 1 wins if there are an odd number of vertices, and player 2 wins if there are an even number of vertices. For a complete graph of order at least 2, player 2 always wins. Complete bipartite graphs are also easy to handle. More interesting are cycles and linear graphs, and I consider these in the next two sections, so don’t read on if you want to think for yourself first.
Cycle graphs
For a cycle, player 2 can always win. How? Player 2 colours green the vertex U that is one place clockwise from the last vertex V that player 1 coloured red. Is it always possible for player 2 to do this? It is only impossible if U is already occupied. But U cannot be occupied by red; else player 1 wouldn’t have been able to colour the adjacent vertex V red. It cannot be coloured green either if the strategy is followed. So player 2 wins.
Linear graphs
For linear graphs, again, player 2 can always win. (Unless the graph has only one vertex.) How? If the graph has an even number of vertices then player 2 can mirror the moves of player 1. I’m sure you see what I mean by this. Here’s a picture to illustrate the effect.
Figure 2. The mirror strategy.
What if there are an odd number of vertices? Player 2 can still win. I have a strategy for player 2 winning, but it’s not as simple as the previous strategies. Generally, he or she should mirror player 1 as before. If player 1 colours the centre vertex, then player 2 colours one of the two vertices adjacent to the centre (which must, necessarily, be empty). There can then arise slight complications moving outwards from the centre as player 1 tries to take advantage of this break in the mirror strategy, but the complications fizzle out. Details omitted; work it out for yourself.
More players
No game theory so far, but when you introduce more players, things get interesting. We introduce a third player, colouring vertices blue. We want to know who loses the game now; who is the first player that is unable to go. Consider the cycle graph with four vertices. The possible outcomes of the game on this graph are shown in Figure 3 (player 1 is red, player 2 is green, and player 3 is blue).
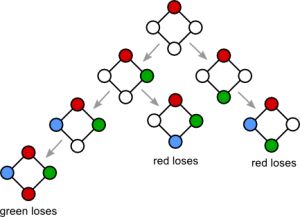
Figure 3. Only red and green can lose this game.
It’s easier (conceptually) using numbers to mark the vertices rather than colours, but the corresponding diagrams look worse. We see from Figure 3 that if green, on his first move, chooses the vertex directly opposite red then red definitely loses. On the other hand, if green chooses one of the two vertices adjacent to red then whether red or green loses is determined completely by blue’s first move. Blue cannot lose. So it makes sense for green to choose the opposite vertex, and red loses.
The five cycle case is better; see Figure 4. I have filtered out various branches from the tree of Figure 4. This missing branches mostly correspond to moves player 3 could make to guarantee he or she loses (when there is a better alternative).
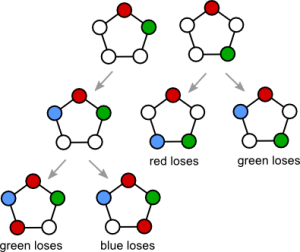
Figure 4. Red, green, and blue can all lose this game.
It seems that green is most likely to lose this game. Indeed, suppose each player adopts the strategy that (i) they wish to maximise their chances of not losing, and (ii) from a selection of vertices with an equal chance of losing, they choose randomly. Then there is a 25% chance red loses, a 50% chance green loses, and a 25% chance blue loses.
Suppose instead these three people are sitting round a table. Green can choose to go down either the left or right branch of Figure 5. If he goes left then who loses depends on red’s next move: either green or blue. If he goes right then who loses depends on blue’s next move: either red or green. So, before green’s first move, red may say to green “go left and I will make blue lose.” At the same time blue may say to green “go right and I will make red lose.” Whichever green chooses, he is saved! Rather than losing with 50% probability, green now has the power to determine who loses the game. Unless, of course, red or blue betray him and make him lose anyway.
What next
What next: I don’t know, this is about as far as I got. Seems worth exploring further. Probably someone else has explored this already! Could make a good set of questions for NRICH.
It was pointed out to me that this game is known, and is called Col https://en.wikipedia.org/wiki/Col_(game)