Ian Short

E left a book, :59 Seconds – Think a little – Change a lot by Richard Wiseman, lying around which stated that people with surnames such as Short, Little, or Bent are especially likely to suffer feelings of social inferiority. (Wiseman referred to some paper or other for this fact.) I laughed, but the author’s surname… The book also suggested that men with positive initials (such as ACE, HUG, and JOY) live longer, and those with negative initials (PIG, BUM, and DIE) die younger. Sounds unlikely. I read the rest of the book, and it was pretty good. Here are some key points from certain chapters (not in order).

Creativity
(1) It’s often thought that brainstorming is more productive than thinking alone. Not necessarily true, because of social loafing. Dominant person doing all the thinking. Guess that’s obvious.
(2) In solving a problem, a good strategy is to leave it for a while, and then return. Your subconscious will have a crack. Various experiments in book to justify this. Seems true. He even suggests that you occupy your conscious mind with a distraction from the problem, and this focussing on something else will help with the original problem.
(3) He has four tips for creativity. (i) Prime: think hard about problem, and then distract yourself. (ii) Perspective: how would X think about this problem? (iii) Play: take a break and have fun. (iv) Ask yourself challenging questions. That’s it. Exaggerated inaccurate summary: to solve a problem work on anything but the problem.
(4) Green things are good for solving problems! Plants. Or without plants paint your room green.
(5) More on priming: try looking at inspirational pictures. These can be great works of art (or listen to music), but a simpler inspirational image is as follows. Consider lots of arrows pointing downwards, and amongst them a single arrow pointing up. Look at this image! It helps you think differently. So the referenced experiments indicate.

Persuasion
(1) Rewards don’t necessarily work – rewards make people believe task must be unenjoyable.
(2) In interviews, likeability is often most important factor.
(3) In the TV programme The Weakest Link, the contestants near the middle win more often. How curious.
(4) To make yourself liked: (i) show interest in others, (ii) ask for favours, (iii) show fallibility, (iv) don’t gossip. All sounds believable.
(5) Here’s one I hadn’t thought of: if you want to get someone to agree to something, first ask them some basic questions they are likely to say ‘yes’ too. Then hit them with your request.
(6) In bargaining, humour helps.
(7) Bystander effect – I like this one. Example is of a guy who collapses in a street. When there is only one other person in the street, he or she offers to help the guy. When there are loads of people,  nobody helps. Reason is because people look to each other for indications of how to behave. So nobody brings themselves to do anything. Also some kind of social embarrassment or something involved.
(8) Reciprocity: help someone and they help you.
(9) Best way of getting a lost wallet returned: keep a photo of a baby in it.

Well that all seemed devious somehow. I’ll move on to…

Happiness
(1) Once reach certain modest level of wealth, happiness independent of money. Believable.
(2) Attempting to suppress thoughts makes them come up more regularly.
(3) After traumatic event, writing about it helps (getting things down in an orderly fashion). Talking may not help though: the orderly part is usually missing. So write!
(4) Writing positive things (in all kinds of contexts) helps you out. Be positive! Wiseman is forgiven for the Short thing. I’ll embrace my surname and ridiculous initials.
(5) If you are happy you smile. Converse holds partly too. Smile and you’ll be happier. Have good posture and use positive language too.

Attraction
(1) The ‘play hard to get’ adage is wrong. Should be ‘play hard to get but at the same time be enthusiastic about the other person’.
(2) Touch a person’s upper arm to be friendly. I won’t be doing that one.
(3) Mimic a person to be agreeable. (What if they catch you?)
(4) Apparently women look for bravery in men and risk taking. Rock climbing number one pursuit for men attracting women. Golf bottom. Aerobics number one pursuit for women attracting men. Body building bottom – ha!
(5) When in love your heart beats faster. Converse holds a bit too. Similar thing with intimate conversations.
(6) Reflected glory: if guy sees girl with guy then guy thinks more of girl than if girl alone.

Decision making
(1) People in groups take more risks. Their views become polarized.
(2) To persuade people, get your foot in the door. Isn’t this in the wrong chapter?
(3) Don’t spend long on big decisions. Let your subconscious work on them. People regret more if they dwell on decisions for a long time.
(4) To detect liars, ignore tension or nervousness; instead look for slow answers, evasiveness, and lack of detail.

Motivation
(1) (i) Plan. (ii) Tell others about plan. (iii) Think about good things that come from achieving goal. (iv) Reward yourself for progress. (v) Record progress.
(2) A familiar phenomenon: once you start a task, your mind wants to finish it, and is agitated until it’s done. Once it’s done, mind wipes it and you can’t remember it so well. (Example, waiter who forgets order once it’s paid.)
(3) Employ Orwellian doublethink: optimism and realism simultaneously.

Stress
(1) Punching and screaming doesn’t help. Instead search for the positive side of things.
(2) Praying for others helps you. Altruism is good for you.
(3) Laugh more. Go outside in the sun. (To alleviate stress.)
(4) Own a dog. (And pass stress on to your neighbours.)

Personality
(1) Apparently its well known that some canny psychologists once went through the dictionary and extracted all the words relating to personality. They then classified those words into five categories, namely openness, conscientiousness, extroversion, agreeableness, and neuroticism. A personality can be well approximated by describing these five attributes.

Parenting
Didn’t read this one.

Relationships
Nor this one.

I recently found the book Letters to my grandchildren, by Tony Benn, in my local library. It consists of a series of short letters written by Tony Benn to his grandchildren, on different political themes.  I like Benn and I like the book. Here are four small parts.

On power and control

Letter 4 is about mechanisms by which leaders control their people. Benn mentions (but does not endorse) the quote ‘democracy inevitably leads to Marxism’ from Mein Kamp. The idea behind this quote is that, in a democracy, the wealthy are a minority, and so everyone else would do well to vote for an even distribution of wealth.

On ignorance

Benn reports that he has told students at ceremonies: ‘When you leave this university you will know far less that there is to be known than when you arrived.’ Benn wasn’t referring to the effects of alcohol; he meant that we cannot keep up with the growth of human knowledge.

On New Labour

Of course there is loads on the Labour Party and New Labour. Benn reports that Margaret Thatcher claimed New Labour was her greatest achievement. (In the sense that, with New Labour, traditional Labour Party values were replaced with Conservative policies.)

On nuclear weapons

Benn is against developing Trident. He describes how our nuclear weapons are dependent on the USA (because we use their technology). So we don’t have an independent nuclear deterrent. He questions whether nuclear weapons work as a deterrent for war anyway, and cites the Falklands war and various other wars. He also mentions money spent on Trident, and the disaster of a nuclear war, as you’d expect.  He says that a person with good sense would not sanction the use of nuclear weapons, and he refers to some wartime officer or other to back him up. In response to this, a prime minister who supports nuclear weapons would have to reassure everyone that he or she would be prepared to use nuclear weapons. That is, the prime minister would be reassuring us that he or she is prepared to approve the killing of millions of people.

Here is an exercise that can be performed with a group of at least three people. Each person secretly writes down a positive integer. The person with the least positive integer that nobody else has written down wins the game. Everyone is aware of the object of the exercise.

There seems to be game theory in this, and statistics. It’s an interesting exercise with which to begin a class. I’ll give it a go sometime and report back here.

Tom Körner gave a seminar here at the Open University a couple of weeks back about using the Baire Category Theorem to prove a quantitative form of a theorem of Rudin. Tom made some passing remarks on the Central Limit Theorem, which I discuss and develop in this post.

Central Limit Theorem. Let X₁, X₂,… be identically distributed, independent random variables with mean 0 and variance 1. Then, for a<b, $latex \displaystyle{P\left(\frac{X_1+X_2+\cdots + X_n}{\sqrt{n}}\in [a,b]\right)\to \int^b_a \frac{1}{2\pi}e^{-t^2/2}dt}.$

This theorem is well used in statistics, finance, and so forth, but as stated above it says nothing about the speed of convergence. It may be that convergence is so slow that the theorem is practically useless. Tom mentioned a related theorem (of Bernstein) which gives an idea of rates of convergence of sums of independent random variable.

Theorem. Let X₁, X₂,… be independent random variables, each with |X_i|≤1 and mean 0. Then, for k>0,
[latex]\displaystyle{P(X_1+X_2+\cdots+X_n\geq k)\leq \exp(-k^2/(4n)).}[/latex]

Sketch proof. First, by expanding out exp(tX_i), we can check that

[latex]\displaystyle{E(\exp(tX_i))\leq \exp(t^2).}[/latex] Let [latex]S_n=X_1+X_2+\cdots X_n.[/latex] Then[latex]\displaystyle{E\left(\exp\left(tS_n\right)\right)\leq \exp(nt^2).}[/latex] Also,
[latex]\displaystyle{P(S_n\geq k)\exp(tk) \leq \int_{S_n\geq k} \exp(tS_n) dP \leq E(\exp(tS_n)).}[/latex] Choose t=k/(2n) and combine the past two equations for the result. ■

I’ll apply this theorem, with certain simplifying assumptions, to the football Premier League. I have written about the Premier League before, in Football Leagues. Each team in the Premier League plays 38 matches. I assume these matches are all independent, and there is no home bias. I will assume that each match is either won or lost (no draws), and 11/4 points are awarded for a win, and 0 for a loss. (The 11/4 points for a win is less than the usual 3, but this compensates well for ignoring draws.)

Let Y₁, Y₂, …, Y₃₈ be the points scored by a particular team. Let us suppose this team has a 50% chance of winning, and a 50% chance of losing. Define X_i = (Y_i-11/8)×8/11. Then the conditions of the theorem above are satisfied and, roughly, we find that

[latex]\displaystyle{P(Y_1+Y_2+\cdots +Y_{38}\geq 1.4k+52)\leq \exp(-k^2/152).}[/latex]
Choose k=30 and we find that

[latex]\displaystyle{P(Y_1+Y_2+\cdots +Y_{38}\geq 94)\leq 0.003.}[/latex]
In other words, there is a less than 0.3% chance that a team from this random league scores more than 94 points. In 2005 Chelsea amassed 95 points, which indicates that teams weren’t all of equal ability in the 2004–2005 season; Chelsea were better than most teams. That is, without knowledge of football, from analysing the distribution of points alone, we see that teams vary in ability.

This quick application of Bernstein’s Theorem was an experiment I carried out through curiosity. There are better ways of analysing football scores.

Some months ago I discussed the following problem with Steve Hewson and Mike Pearson after an NRICH meeting. Two people play a game with a finite graph. They take turns in colouring the uncoloured vertices of the graph, one vertex at a time. One player colours vertices red, and the other player colours vertices green. Two adjacent vertices (vertices joined by an edge) cannot be coloured in the same way. The loser of the game is the first person who is unable to colour a vertex.

Figure 1. Green is unable to colour a vertex.

The optimal strategy for each player depends on the graph. For a graph with no edges, player 1 wins if there are an odd number of vertices, and player 2 wins if there are an even number of vertices. For a complete graph of order at least 2, player 2 always wins. Complete bipartite graphs are also easy to handle. More interesting are cycles and linear graphs, and I consider these in the next two sections, so don’t read on if you want to think for yourself first.

Cycle graphs

For a cycle, player 2 can always win. How? Player 2 colours green the vertex U that is one place clockwise from the last vertex V that player 1 coloured red. Is it always possible for player 2 to do this? It is only impossible if U is already occupied. But U cannot be occupied by red; else player 1 wouldn’t have been able to colour the adjacent vertex V red. It cannot be coloured green either if the strategy is followed. So player 2 wins.

Linear graphs

For linear graphs, again, player 2 can always win. (Unless the graph has only one vertex.) How? If the graph has an even number of vertices then player 2 can mirror the moves of player 1. I’m sure you see what I mean by this. Here’s a picture to illustrate the effect.

Figure 2. The mirror strategy.

What if there are an odd number of vertices? Player 2 can still win. I have a strategy for player 2 winning, but it’s not as simple as the previous strategies. Generally, he or she should mirror player 1 as before. If player 1 colours the centre vertex, then player 2 colours one of the two vertices adjacent to the centre (which must, necessarily, be empty). There can then arise slight complications moving outwards from the centre as player 1 tries to take advantage of this break in the mirror strategy, but the complications fizzle out. Details omitted; work it out for yourself.

More players

No game theory so far, but when you introduce more players, things get interesting. We introduce a third player, colouring vertices blue. We want to know who loses the game now; who is the first player that is unable to go. Consider the cycle graph with four vertices. The possible outcomes of the game on this graph are shown in Figure 3 (player 1 is red, player 2 is green, and player 3 is blue).

Figure 3. Only red and green can lose this game.

It’s easier (conceptually) using numbers to mark the vertices rather than colours, but the corresponding diagrams look worse. We see from Figure 3 that if green, on his first move, chooses the vertex directly opposite red then red definitely loses. On the other hand, if green chooses one of the two vertices adjacent to red then whether red or green loses is determined completely by blue’s first move. Blue cannot lose. So it makes sense for green to choose the opposite vertex, and red loses.

The five cycle case is better; see Figure 4. I have filtered out various branches from the tree of Figure 4. This missing branches mostly correspond to moves player 3 could make to guarantee he or she loses (when there is a better alternative).

Figure 4. Red, green, and blue can all lose this game.

It seems that green is most likely to lose this game. Indeed, suppose each player adopts the strategy that (i) they wish to maximise their chances of not losing, and (ii) from a selection of vertices with an equal chance of losing, they choose randomly. Then there is a 25% chance red loses, a 50% chance green loses, and a 25% chance blue loses.

Suppose instead these three people are sitting round a table. Green can choose to go down either the left or right branch of Figure 5. If he goes left then who loses depends on red’s next move: either green or blue. If he goes right then who loses depends on blue’s next move: either red or green. So, before green’s first move, red may say to green “go left and I will make blue lose.” At the same time blue may say to green “go right and I will make red lose.” Whichever green chooses, he is saved! Rather than losing with 50% probability, green now has the power to determine who loses the game. Unless, of course, red or blue betray him and make him lose anyway.

What next

What next: I don’t know, this is about as far as I got. Seems worth exploring further. Probably someone else has explored this already! Could make a good set of questions for NRICH.

The following problem was suggested by Bernard Murphy at Jenny Piggott’s retirement meeting in Cambridge on Tuesday 13 July.

Problem

Consider eight jacket buttons in a column, as shown on the left hand side of the image below.

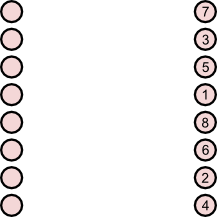
We can unbutton the eight buttons in various orders; one such order is shown on the right hand side of the above figure. The problem is to choose an ordering so that we have to move up and down the buttons the maximum number of times. For example, if we unbutton in the usual fashion, starting from the top button and finishing with the bottom button, we would make in total seven moves (from first button to second button, from second button to third button, and so forth). In the example above, we travel from button 4 to button 7 (3 moves), then button 7 to button 2 (5 moves), and so forth, totalling 31 moves.

Bernard’s question was What is the maximum number of moves? We add to that question Which unbuttoning strategies yield this maximum?

Solution

I’ll state the answers here, and prove them below. The maximum number of moves is 31. One unbuttoning strategy which yields this solution is shown above. What do the others look like? They can all be described as follows. The four odd labels 1, 3, 5, and 7 must all occur in either the top four, or bottom four, positions. Also, labels 1 and 8 must occupy buttons 4 and 5, in either order.

Reformulate the problem

A suggestion made at the time was to regard this as a graph theory problem. Let the buttons represent the vertices of a weighted complete graph, and the weight between two buttons is the number of moves it takes to get from one button to the other. The original question then becomes a special case of a travelling salesman problem. I see this perspective as a significant backwards step; we have moved from a simple linear graph to a complicated complete graph, and I won’t discuss this view any further.

A more obvious graph theoretic model is to consider the buttons to be vertices of the linear graph shown below. If we equip this graph with the usual graph metric d, then the problem is to choose an ordering v₁,…,v₈ of the vertices such that the quantity d(v₁,v₂)+d(v₂,v₃)+…+d(v₇,v₈) is maximised.

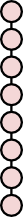
A third form of the problem is to choose an ordering x₁,…,x₈ of the integers 1,…,8 such that the sum |x₁-x₂|+|x₂-x₃|+…+|x₇-x₈| is maximised. (Here x_i is the number of the ith button chosen.) I solve this problem in the next section.

Explanation of solution

We first solve a more symmetric version of the last problem, which is to choose an ordering x₁,…,x₈ of the integers 1,…,8 such that the sum |x₁-x₂|+|x₂-x₃|+…+|x₇-x₈|+|x₈-x₁| is maximised. There is an extra final term in the sum, which corresponds to moving from the finish button back to the start button.

Let S=|x₁-x₂|+|x₂-x₃|+…+|x₇-x₈|+|x₈-x₁|. The numbers 1,…,8 each occur twice as terms x_i in this sum. Consider, for each i, reordering the terms x_i and x_i+1 from each summand |x_i-x_i+1|, if necessary, so that the modulus sign can be removed without affecting the value of S. We end up with eight +x_i terms, and eight -x_i terms. The maximum value of S is attained if and only if the eight plus terms are 5, 6, 7, and 8 (each twice) and the eight minus terms are 1, 2, 3, and 4 (each twice). Thus this maximum is attained if and only if we repeatedly alternate between the top four and bottom four buttons. The maximum has value 2×((5+6+7+8)-(1+2+3+4))=32.

Our simpler, but less symmetric, problem cannot, therefore, have value greater than 31. Since we know that 31 can be achieved, it is the maximum value for the problem. To obtain all the orderings which yield this value 31 we simply select those solutions which have |x₈-x₁|=1. Now, |x₈-x₁|=1 if and only if x₁ and x₈, the start and finish buttons, occupy the middle two button positions.

Comments on solution

I haven’t gone into detail above; nor have I taken much care in my explanation. The method generalises to n buttons, and you should find that ½floor(n²)-1 is the maximum number of moves. I haven’t worked out the number of solutions which achieve this maximum, but one could easily do so.

Extensions

The most natural extension is to choose a graph G equipped with the graph metric d and investigate what ordering of the vertices v₁,…,v_n of G maximises the sum d(v₁,v₂)+d(v₂,v₃)+…+d(v_n-1,v_n). It’s easy for a cycle, and probably easy for a tree. Later note: I worked out the details for a tree, and may publish the results somewhere.

How quickly can a number of people, each with an unlit candle, light their candles from a single lit candle? This problem presented itself during a service in St. Mary’s Church in Maynooth, Ireland, to which I was kindly invited on Holy Saturday (3 April 2010). The congregation were seated in a block, and each person had an unlit candle. A single large lit candle sat in front of us and from this candle an altar girl lit her own portable candle. She then walked round the outside of the block of people lighting their candles one by one. Once a person’s candle was lit, they could light the candles of their neighbours. Soon everybody’s candles were lit. The situation is modelled in the diagram below.

The grey circles represent members of the congregation with their unlit candles. The altar girl is the circle at the front with a yellow (lit) candle. The altar girl proceeded clockwise around the block of candles, and they were lit as suggested by the following figure. (There were not actually eight rows of eight people; I don’t know how many people there really were.)

This can be considered as a discrete optimisation problem. The task is to light all the candles in the smallest possible time. At each stage of the model, each static member of the congregation can light the candle of one of the at most eight people directly surrounding them. Likewise the mobile altar girl can also light the candle of any one of the at most three people directly surrounding her, but she can also walk round the congregation block. Let us say that she can walk five steps up, down, left, or right during the time it takes to light a neighbour’s candle. What strategy should the congregation employ to light their candles as quickly as possible?

Let us ignore the altar girl for the moment, and suppose simply that the static person in the top right corner begins with his candle lit. He lights the candle of a neighbour, then he and the neighbour light the candles of a neighbour each, and so forth. So we see that on the kth stage, no more than 2^k candles can be lit. Thus, given a block of n by n people, it will take at least 2log₂(n) stages for all their candles to be lit. Since we have the constraint that a person can only light the candles of his or her neighbours, it is unlikely that this bound can be achieved. In fact, I think the optimal (fewest) number of stages is n+1, which is achieved using the strategy indicated by the next figure.

I doubt this bound can be beaten – at least, not by more than 1 – even if we adjust the person who initially has his or her candle lit. For an m by n group of people, I conjecture that the optimal number of steps is, in general, max(m,n)+1.

Introducing the altar girl increases the difficulty of the problem. Perhaps she should light the candle of one person, person A, near the centre of a side, and then walk all the way round to the other side and light the candle of the person directly opposite person A. I have yet to consider the problem in depth.

A typical night in Johannesburg?

G and I were driving back from a music club in Jo’burg at 1am when we came across a woman who had driven into, and felled, some traffic lights. We pulled up alongside her and asked whether she was okay. She said no, and then pulled away. She didn’t get far because her bumper was hanging off and was tangled up with her front wheel. She ground to a halt in the middle of a cross-roads junction, which in the day time is a busy intersection. We moved off to park fifty metres down the road, and as we walked back to meet (and help) her, a guy pulled up nearby, and she left her mangled car, and drove off with him. We noted the guy’s number plate.

She locked the doors of her battered car when she left, and it was stuck in the middle of the junction. There was glass, traffic lights, and mess. Local kids were hanging around and joking about stealing the car. Two other groups quickly arrived on the scene. The first were the vulture tow trucks. These are guys in tow trucks who search the streets of Johannesburg for broken down vehicles to tow away. They must work on commission. Also around, but less interested in the action, were private security patrols who work for local wealthy residential groups. A block of houses may get together and employ a security patrol to monitor their neighbourhood. These security cars came and went; mostly, they weren’t interested. One of them drove 300 metres down the road to the police station, to see if the police would come out to sort things out. (The police had been phoned earlier, but weren’t up to much.)

We waited by the abandoned car – me and G, two vulture trucks, a couple of private security cars, and a load of kids – and then a woman drove past us, continued about 200 metres, then swerved across the opposite side of the highway into a wall, which collapsed. In an instant, the vulture trucks were after her. I’m not sure whether they were keen to help, or keen to claim the latest wreck. Everyone else went off to see the recent crash, and left only me and G by the original car. After twenty minutes or so, with more vulture trucks and security cars and various others turning up, G and I went to see the new crash. A single drunk woman had knocked down the wall, destroyed her car, but luckily lived. The metro cops had arrived at this crash (traffic police), and they were talking with the owner of the wall, who was worried about the direct route into her back garden. Kids were teasing the car crash woman for being drunk. The metro cops weren’t bothered about people hanging around. They didn’t seem bothered about anything. We tried to give them the number plate for the other crash, but they weren’t interested.

Later on we returned to the original crash and found the mother and brother of the traffic light crash woman. They had come to sort things out. “She never does anything like this.” About one hour after the first crash, the police showed up. They looked bored. We left soon after.

The following day, a couple of blocks away, I saw that another set of traffic lights had been felled.

Here are some problems I developed for NRICH on disconnecting sets of points.

Introduction

There is an island, shown below, which contains five towns, each marked by a coloured disc. The people from the red towns are arch rivals with the people from the blue towns, so they decide to build a wall to separate all the red towns from all the blue towns. The red towns want to stay in contact with each other so the wall must not separate two red towns. Likewise the wall must not separate blue towns. The wall must be continuous, it must not intersect itself, it must not split, and each end of the wall must be at a point on the coast. Let us call such a wall a dividing wall.

Is it possible to construct a dividing wall? Yes, one is shown below.

If you manage the above example, then perhaps you can answer the following question. Given any configuration of red and blue towns, is it always possible to build a dividing wall?

Coastal towns

The next island (below) has coastal towns. These towns differ from all previous towns as you cannot encircle each one with a wall. Can you separate the red and blue towns with a wall in this example?

Have you managed it? If not then persevere; it is possible! Try the next example.

If you cannot build a suitable wall for the previous example then try to answer the following question. What is the simplest configuration of towns, both coastal and inland, for which you cannot build a dividing wall?

Once you have answered that question you may try this harder question. Can you characterise those configurations of towns for which it is possible to build a dividing wall?

Building roads

History is littered with examples of dividing walls that have contributed to war and misery. Let us suppose that the people from our five original towns are more enlightened, although retain their animosity towards each other. Rather than building a wall, they decide to build two roads. One road connects all the blue towns, and the other road connects all the red towns. The two roads are not allowed to intersect themselves, or each other. The blue road starts at a blue town, and then passes through each of the other blue towns, finishing at a blue town. Likewise for the red road and the red towns. Let us call a pair of such roads connecting roads. An example of a pair of connecting roads is shown below.

Here is a pair of connecting roads for the first coastal town example.

Are the problems of building a dividing wall, and building a pair of connecting roads, related?

More towns

Recent immigrants to the island have set up their own green town. The unfriendly locals quickly found reason to dislike them, and now the dividing wall must separate red towns, blue towns, and green towns.

It is impossible to separate all three sets of towns with one dividing wall. We need another! The rules for two dividing walls are that they must not intersect each other, and each end of each wall must start either from a point on the coast, or from a point on one of the other walls. We can separate red from green from blue with two dividing walls, as shown below.

We can bring in green coastal towns too, and address the next question. Which configurations of red, green, and blue towns can be separated by two dividing walls?

Questions and answers

Questions. Does the shape of the island affect the problem? How about if we introduce lakes to the island, across which neither walls nor roads can be built? We can allow more roads and walls. Does that actually help? We can introduce more towns too. Also, we can assume that the island is a sphere, rather than a disc shape. (That is, we can ask the same questions for people on the whole Earth.) Or we can assume that the people live on a torus. Unlikely, but don’t let that hold us back. We could consider multiple islands, and build bridges between them.

Answers. I haven’t worked out all the answers! The shape of the island doesn’t matter, so we may as well assume it is a disc. Lakes have no impact; we can shrink them down to points without affecting the problem. For two colour types, if there are no coastal towns then a dividing wall exists. If there are coastal towns then a dividing wall exists unless there are four coastal towns that occur in the order red, blue, red, blue, clockwise around the island. Connecting roads are the same as dividing walls. The reasons are similar, if not exactly the same as, the idea in metric space theory of equivalence of path connectivity and connectivity. I don’t imagine that extra walls would help with the two coloured towns problem. For n colour types, and n-1 dividing walls, I suspect that for successful configurations, same coloured towns must be grouped together round the coast.

Yesterday it snowed and I made an arch from the snow.

Some local kids helped for a while, before attacking me with snowballs. Later on that evening, after a long patient wait with Ellie’s camera, I caught the perfect shot.

A unique moment. The following day some more local kids &#8211; possibly the same ones &#8211; arrived with a broom and destroyed the arch. They fought with the broom in my front garden for five minutes, and then left, forgetting the broom.

For more on wolves, see all about Wolves.