Mathematics Education

On Friday 9th March, we hosted the very first Open University Mathematical Resilience Day for students in year 9 in the Hub Theatre on campus. The day was aimed primarily at girls with a focus on building their mathematical resilience. Students from schools in and around Milton Keynes were invited to attend the event, which was funded by a grant from the London Mathematical Society (you can find out more about the LMS here: https://www.lms.ac.uk/).

Throughout the day, our focus was to support students to develop as resilient learners, through working together and discussing strategies to help them when they found the mathematics challenging. Alongside working on mathematical problems, we discussed three key aspects of mathematical resilience:

1. Growth zone model
2. Growth learning theory
3. Growing mathematical resilience

The students started the day by completed an attitude to learning questionnaire, based on the Fennema-Sherman Mathematics Attitudes Scales, encouraging them to think about the way they think about learning.

1. Growth Zone model

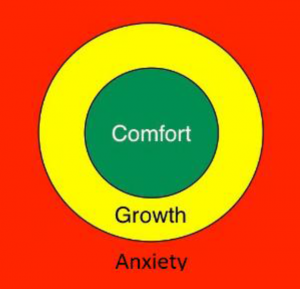
Clare introduced the Growth Zone model, a concept introduced in her work on mathematical anxiety and mathematical resilience

In the GREEN zone you are comfortable. You might be consolidating some ideas but you are not learning. 

In the YELLOW (or amber) zone you are learning, but learning feels risky and a bit uncomfortable, there are barriers to overcome, there is some struggle and you have to perserve to be able to “get it”. Stay here as long as you can, you will learn more that way, but don’t stay too long. 

In the RED zone the risks feel too great, you feel unsafe and anxious. The barriers feel too much, you just cannot do this. You need help. Don’t be afraid to ask for what you need.

Working on some mathematical problems using the Growth Zone model

The girls were encouraged to use their “growth zone” models throughout the day to chart how they felt about each activity and to help them to talk about their feelings in relation to the mathematics they were doing.

You might like to have a go at the task below yourself. If you do, why not chart your feelings using the Growth Zone model shown above?

Task: 9 coloured cube

If you have 27 cubes, 3 each of nine colours (e.g. 3 yellow, 3 blue etc).

Can you make a 3 by 3 by 3 cubes so that each face contains exactly one of each colour?

The image above shows a cube with two faces that meet this criteria, but unfortunately on the third face there are two green cubes and two black cubes, so this is not a solution.

You can find this task, and other similar problems here: Nrich.org.

2. Growth Learning theory 

Clare explained that, according to Growth Learning theory, there are two ways in which people think that they learn:

1.Fixed Theory of Learning: I can only learn just so much, no matter what help and support I get I really won’t make much progress in maths.

2.Growth Theory of Learning: I have the confidence that I can develop mathematical skills. I know that everyone can learn more mathematics with effort from themselves and support from others and that includes me.

Neuro-science tells us that the brain grows every time you use it – it makes more synapses and connections but if you don’t use it those connections are pruned. Grow your brain!

“Being Stuck is an honourable state”

John Mason, Emiritus professor at the Open University, wrote in 2014: “Everyone gets stuck sometimes, and it can be frustrating, even debilitating rather than stimulating. However, being stuck is an honourable and useful state because that is when it is possible to learn about mathematics, about mathematical thinking, and about oneself”.

We discussed the importance of “being stuck” in mathematics and talked about the fact that even very successful mathematicians get stuck sometimes. For instance, world-famous mathematician Andrew Wiles, who gained fame by solving a nearly 400-year-old, previously “unsolvable” problem: Fermat’s Last Theorem, recently spoke in an interview about the “state of being stuck”. In this interview, Andrew Wiles was asked what advice he would give to the general public about mathematics, his answer was “accepting the state of being stuck.

Having identified that “being stuck” would be inevitable at some point and reflecting on the way they worked together, the girls created “STUCK” posters, which were filled with advice for themselves and others, including “Don’t give up”, “Teamwork is key” and “keep practising”.

One group came up with an acrostic poem to help students when they are STUCK:

• Stop
• Think
• Underline key words
• Communicate
• Keep trying

Having the confidence to question what you read: Numbers in the News

After lunch students were treated to a talk entitled “Numbers in the News”, given by Zoe Griffiths from @ThinkMaths who showed them misleading graphs and charts used in newspapers, leaflet campaigns and social media to give biased information. Her aim was to show the students that they can learn to use mathematics to critically review the information that they read and hear about.

Zoe also talked about the importance of knowing sample size and methods of data collection used before deciding whether a claim is credible.

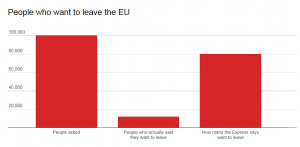
For example, one newspaper claimed that 80% of people wanted to leave the EU. Looking into the detail of the poll, data was collected in only three constituencies and a leaflet campaign preceded the poll. In addition, out of 100,000 people who were asks, only 14,851 responded to the poll, of which 11, 706 voted to leave. This graph, published by the Independent online, demonstrates the newspaper’s claim and the actual quantities of responses.

To further exaggerate the point, Zoe showed a Tweet claiming that “100% think cats are the best”  (from a sample size of two: one person and their cat).

Zoe’s talk emphasised the importance of having confidence in our own mathematical abilities in order to interrogate data presented to us in the news, social media and advertising.

She finished the session with a demonstration on not being fooled by “special offers”! Girls were tempted with winning £20. I won’t spoil the game here, but you can get in touch with Zoe to find out more! @thinkmaths

You can find out more about the talks Zoe and her team offer for schools and events here: http://www.think-maths.co.uk/.

Student task: Analysing the validity of newspaper claims

Following Zoe’s talk on interpreting data in the news, the girls were given a task to identify whether there was enough evidence to support claims made. The students worked together, using strategies from their stuck posters to support each other, to organise and interpret the data given and to justify their decisions.

Have a look at some of the statements below

3. Growing mathematical resilience

Finally we invited the students to reflect on whether they have mathematical resilience. Clare explained that, if you have mathematical resilience you will:

• seek to stay in your growth zone, get help when you need it and avoid the red zone where you know you cannot think;
• feel part of an inclusive community of those who are learning mathematics and understand the value of doing so;
• know that sometimes there are barriers to understanding mathematics which you have to struggle over;
• persevere, knowing how to overcome difficulties, and how to get the help that you need;
• work collaboratively with your peers giving and receiving help to push ideas forward;
• work to use the language needed to express what you understanding, misunderstand and to ask questions;
• have a growth theory of learning, that is you will know that the more you work at mathematics, with support, the more successful you will be.

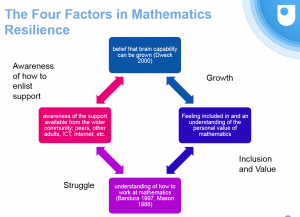
To summarise, in order to be able to develop Mathematical Resilience you need:

1. To believe that brain capacity can be grown (Dweck, 2000)
2. To have an understanding of the personal value of mathematics
3. To understand how to work at mathematics
4. To have an awareness of the support available from the wider community, including: peers, teachers, school resources and the internet.

Reflecting on the day

The students reflected on what they had learned throughout the day, returning to an attitude to learning survey which invited the students to review whether their feelings towards leaning had changed as a result of the activities and discussions throughout the day.

Here are some of the questionnaire responses to the question: Has anything changed in your beliefs concerning learning mathematics? 

“That if I believe in myself I can do it.” 

“Maths is not that difficult if you ask for help and try it.”

“I shouldn’t give up! I should keep on trying!”

When asked to write down the three key ideas which the students felt helped them solve mathematical problems during the day, responses included:

• Teamwork
• Perseverance
• Patience
• Asking for help
• Confidence
• Your growth zone
• Breaking up the question
• Read the question carefully
• Don’t give up straight away
• Trial and error
• Stop and think
• Count to 10
• Discussing worries/strategies
• Writing down calculations
• Having fun!

The students appeared to leave tired but happy, taking away with them the strategies used in each of the activities and a laminated growth zone model!

Further exploration

If you want to find out more about Clare’s work with Sue Johnston-Wilder on mathematical resilience, you can visit their website here: http://www.mathematicalresilience.org/.

On January 16th the Mathematics and Statistics department at the Open University hosted a talk by Dr Clare Lee on mathematical resilience. The construct of mathematical resilience can help teachers to support learners of mathematics to develop the resilience to overcome barriers to mathematics learning such as anxiety about mathematics. It arises from what Bandura describes as self-efficiacy; the belief that one can overcome difficulties and successfully solve problems (such as learning hard things in mathematics).

Clare Lee, along with her colleague, Sue Johnston-Wilder, have developed a diagrammatic representation of three zones which can be used with learners to help them identify their current feelings towards mathematical learning. The comfort zone is an area where learners are probably not learning new mathematics, as this is an area of mathematics they have already mastered. The anxiety zone is an area where learners feel that the mathematics is too difficult and they tend to give up and not try. In between is the growth zone where learning occurs; there is enough challenge that the learner has to develop new skills, but the challenge is not too great as to cause the learner to panic. Using the diagram gives teachers and learners a way to promote staying in the growth zone so that learners can make progress in mathematics and develop the confidence to continue to make progress.

Find out more

Are you interested in finding out more about mathematical resilience?

The literature referred to in this blog post is here:

• Bandura, A. (1997). Self-efficacy: The exercise of control. New York: Freeman.
• Lee, C. & Johnston-Wilder, S. (2013) Learning Mathematics- letting the pupils have their say, Educational Studies in Mathematics, Vol 83 (2), 163-180

Clare Lee has also written about developing mathematical resilience in teachers which you find out about here: https://www.open.ac.uk/blogs/per/?author=63.

 Mathematical Resilience Event

On Friday the 9^th March, Clare Lee and Charlotte Webb will be hosting a Mathematical Resilience day on the Open University campus in Milton Keynes for year 9 students from the local area. The day is aimed primarily at girls and is targeted at those who feel under confidence with mathematics. During the day the students will use the growth model image shown above and will work on strategies to become resilient learners.

If you are a Teacher of mathematics or Head of department in the MK area and you are interested in bringing some students to this event, please get in touch via email: [email protected].

Hi, I am Harry Gretton and, at present, a tutor on ME625 and other “M” courses. I have been an OU tutor since the Open University began! and have tutored continually on many varied “M,T and E” courses.

In parallel with this I worked for Sheffield Hallam University for even more years teaching mathematics, statistics and computing to a wide diversity of students and many different levels. Throughout this I have always being particularly interested in “what is doing mathematics now that technology is here”. https://www.gretton.net/Papers/ATCMA161.pdf  and the way mathematical skills are assessed.

The changes in the teaching and use of mathematics will always continue since “Some Mathematics becomes more important because technology requires it. Some Mathematics becomes less important because technology replaces it. Some Mathematics becomes possible because technology allows it” Bert Waits – 2000.

I used to play squash and rugby to a reasonable level but have retired due to some physical reconstruction. Since retiring from Sheffield Hallam University I fill my spare time? looking after a small holding and doing regular grand parenting duties. …

_______

Sue Forsythe

I have always liked solving maths puzzles and nowadays I am a fan of killer Sudoku. My Saturday morning routine is to solve the futoshiki and the killer Sudoku in the Guardian newspaper. I also like getting my hands on a good kakuru.

Mathematics in Art is another passion. I especially enjoy studying designs with symmetry in them. Symmetry appreciation is a human attribute which even babies partake in. Ask me for the reference sometime.

I also like playing the bass recorder in a recorder ensemble, knitting and occasionally creating a bit of craftwork. A sense of symmetry underlies both music and art and craft.

_______

Gerard Hayes

Hello everyone,

I have been a tutor on all ME modules since their inception. I have also tutored ME830 and ME831, and the residential school MEXR624.

Previously I have taught maths in secondary schools. I was appointed as an Advanced Skills Teacher prior  in to moving into advisory work then teacher education and training most recently on the secondary maths PGCE at Edge Hill university.

My  degrees were all obtained as a part time student while working full time, one was with the Open University.

My main hobbies are singing and operating as a volunteer at Lyme Park with the National Trust.

_______

Charlotte Webb

Before moving to the Open University, I was a secondary mathematics teacher in Bristol, Oxford and most recently in Madrid. I have also worked with primary and secondary aged children through delivering workshops and masterclasses with the Royal Institution and at Bletchley Park.

My Master’s degree in Mathematics Education looked at the way children use proof and reasoning in mathematics. I am interested in the way teachers can work with children to support them in becoming mathematicians and thinking mathematically, through using the ideas in our modules, such as conjecturing and convincing, within the classroom.

Alongside mathematics, I love painting, drawing and all things arts and craft. I am particularly happy when maths and art come together, for example in M. C. Escher’s tessellation pictures. I have just started an Islamic geometry art course, which I am excited to share with you in a blog post soon!

In my free time, when not getting crafty, I love to travel and enjoy seeing live music and comedy – the Edinburgh Fringe festival is one of my favourite places to be. I also have a miniature sausage dog called Ronnie!

_______

Jeffrey Goodwin

As well as being an Associate Lecturer for ME627, I also tutor on ME620 and ME626. I first worked as a tutor for the OU in the 1980s on EM235 Developing Mathematical Thinking and returned to my current role of Association Lecturer in September 2014.

I was a classroom teacher for 10 years, working in Secondary and Middle schools. I moved into the advisory service in 1980 as Head of the Hertfordshire Mathematics Centre. I worked in Initial Teacher Training and running CPD courses for teachers; being head of mathematics education at Anglia Polytechnic University. For four years from 1986, I worked for the National Curriculum Council on a curriculum development project: Primary Initiatives in Mathematics Education (PrIME). I have always had an interest in assessment and testing and in 1998 was appointed to establish and lead the Mathematics Test Development Team at the QCA. We developed the end of key stage tests and other optional tests for all three key stages. I was in this role for eight years and then moved to research when I was Head of Research at Edexcel and then Pearson Research and Assessment. In 2010, I became an independent consultant and worked with schools on making changes, particularly engaging with Japanese Lesson Study. For four years I was the Programme Director for the King’s College London MaST course.

I have seen it as important to make a professional contribution to education. This has involved being Secretary of the Mathematical Association, a member of the Royal Society Mathematics Education Committee and Chair of the coordinating committee for Primary Mathematics Year 1988. I have also been chair of governors of a primary school.

I have two main research interests: the role that Lesson Study plays in the profession development of teachers; and, a member of the research team at the UCL Institute of Education looking at The Nature, Prevalence and Effectiveness of Strategies used to Prepare Pupils for Key Stage 2 Mathematics Tests, a project funded by the Nuffield Foundation.

_______

Angie McConnell 

I’m Angie McConnell and I am currently a tutor on ME620 and ME625. I have been an OU tutor since 2005.

However, my connection with the OU stretches back a very long way – my first degree was from Liverpool University then in 1978  I started an OU degree and followed that with an MSc with the OU – all in Mathematics so I do understand what it is like to be an OU student. I taught for 10 years in a Secondary school then for 30 years in an FE college teaching a wide range of students but always Mathematics. The classes I loved were adult students, many of whom had a genuine fear of mathematics, and I am proud to say I converted many a ‘I hate maths’ student to an ‘it’s all right this maths stuff isn’t it?’ student.

In my spare time I love to travel and explore new places and countries and there’s usually an opportunity to do some maths. Sitting next to a young girl on a train in a remote part of Thailand I realised that she was struggling with her maths homework on quadratic equation. I offered to help and between us we sorted it. She spoke very little English and I speak even less Thai, but mathematics is a universal language.

I have two cats who are very helpful when it comes to marking TMAs and EMAs and love to walk across the keyboard as I am typing so if your feedback is returned with strange typos blame the cats.

_______

 Pete Kelly 

I have been a mathematics education tutor with the OU since 2013, and teach on all four of the Mathematics education modules. I have also studied with the OU myself, and so understand some of the challenges part-time distance-learning students face. As well as teaching with the OU, I am Reader in Comparative Education at Plymouth University. I am particularly interested in understanding mathematics classrooms, and have been lucky enough to travel to countries across Europe to compare how mathematics is taught. Before moving into higher education, I spent fifteen years working in primary and middle schools in London and South West England including five years as a deputy head and five as a head teacher.

_______

Wendy Troy

I tutor on both ME626 and ME627 modules, both since their inception. I have also tutored ME620 and ME830, and the residential school MEXR624, now sadly stopped.

Previously I have taught maths in secondary schools and a further education college. I then moved into advisory work then teacher education and training most recently on the secondary maths PGCE at IOE London and Goldsmiths.

My first degree was in Economics, my MA in Psychology of Education and later I gained an Honours Maths degree with the Open University.

The History of Maths is one of my enthusiasms together with maths from all over the world.

_______

Tom Cowan

I have been an Associate Lecturer with the OU since 2008 when I worked on the MEXR624 summer school each year in Bath.  When that ended I was lucky enough to be offered a chance to work on ME625 which led to tutoring on all the 4 modules which we offer in the Mathematics Education suite of modules at Level 3 and also working on the Masters module ME825.

I completed my Master’s Degree with the OU in 2010 so remember what it was like to study at a distance and cramming in study whilst jugging other things in life.

My full-time role is as the Programme Lead of an initial teacher education programme at the University of Plymouth.  I support the education and development of new Primary teachers on the BEd and PGCE – looking after those students with a specialism in mathematics.  Prior to this I was primarily involved with working with Secondary and Primary schools to support them with mathematics in challenging inner-city schools around Manchester and Salford.

I’ve never really left education and have found my next challenge in aiming to complete my Doctorate in Education in 2022! Hopefully I’m well on my way to becoming Dr. Cowan!

When I have some spare time, I enjoy going to the theatre, supporting Liverpool FC and Widnes RLFC and work as an officer with the Boy’s Brigade which keeps me in touch with further voluntary work (I did say spare time right?)

_______

Cathy Smith

I started as a secondary mathematics teacher in Hertfordshire and Suffolk, where my Head of Department noticed that my name could be anagrammed as itchy maths. I embraced this by moving roles within education, while always keeping a central interest in maths itself.

I have worked in the field of mathematics teacher education since 1993, in Cambridge, London and now at the Open University.  My professional and research interests lie in participation in advanced mathematics, and teaching for an inclusive mathematics.

My PhD was a poststructural analysis of the discourses of mathematics and further mathematics. I have been involved with British Society for Research in Learning Mathematics, the Further Mathematics Support Programme, and am a member of both MA and ATM.  Outside of work I like singing and making things (knitting, lace, Lego), sometimes simultaneously.

_______

Jim Thorpe

I became a mathematics teacher through the accident of joining Bill Brookes’ PGCE course: suddenly I realised that much mathematical thinking could emerge from humble beginnings, numerical or geometrical, and realised that mathematics could make a major contribution to the intellectual and social development of adolescents if they were encouraged to function as young mathematicians within what John Mason calls a ‘conjecturing atmosphere.’

I have been committed to mathematics education for a long time, in the secondary classroom and then in a variety of ways supporting the work of mathematics teachers. My current occupation is mainly tutoring in mathematics and education, mathematics, and engineering for the Open University.

I am alarmed by much of what I see under the heading of teaching mathematics but remain unrepentant in proposing something richer than the all-too-frequent ‘training’ metaphor of communicating mathematics.

This is a time of year when I pay attention to ribbons and wrapping paper.

When I saw this  oak leaf ribbon, I had to buy some – just because of its beautiful symmetry.

But what kind of symmetry is it?  Thinking about this question reminded me of Bob Burn, a mathematics teacher educator, who introduced me to reasoning about algebra-geometry in a pleasurable, visual way . So that’s the thread of this blog, which is more about mathematics I enjoy than mathematics education.

Ribbons are like friezes, or decorative borders that appear on walls.  They become mathematical when they have a regular repeat in them. There is a section (the ‘motif’) that is ‘translated’ – let’s say moved horizontally – again and again to make the whole repeating pattern. It needs to be translated by the same distance each time: on this ribbon it’s about 3cm. Of course this is a sensible way of manufacturing them.

Every mathematical frieze has a basic translation symmetry defined by the pattern repeat; let’s call it T.  If I translate the frieze using T it looks the same, since all I have done is moved it along by exactly one repeat.  From now on I won’t worry about where the ends of the frieze are:  I am just going to think about its middle, or say it is infinitely long. Then I can say T ‘leaves the frieze invariant’.  In our OU mathematics education modules that’s called finding invariance in the midst of change: the translation is the change, but the overall appearance has not varied.

Here’s another ribbon with a repeating pattern of red and white checks. This time T is a translation of about 3.2cm. I can also see this ribbon has a horizontal line of reflective symmetry along its length. That means there is a horizontal reflection (call it H) that would just swap the top and bottom in the line of symmetry but again leave it looking the same overall.

It has other symmetries as well: I can see a vertical line of symmetry through the central one of each group of 3 white stripes, and through the middle of each red space.  So there are also vertical reflections V that leave this pattern invariant.

And there is rotational symmetry R as well.  Every frieze has rotational symmetry of 0ᵒ or 360ᵒ – that is not interesting – but it is possible to rotate this ribbon just by 180ᵒ and leave the pattern invariant.  What I have to do is choose the centre of rotation to be in the very centre of a red rectangle, or the centre of a middle white stripe. That is exactly where the vertical lines of symmetry meet the horizontal one (coincidence?).

This ribbon has four symmetries that leave it invariant: T and also H, V and R.  It’s got so much symmetry that it looks neat and crisp, but may be a bit boring.

There’s one more useful thing to notice about it though: in principle you could choose the motif as being any section of ribbon that is 3.2 cm long. I’ve put four example sections in the picture; each of these works since translating that section gives the whole ribbon. But only two of those motifs have got the same other symmetries as the whole ribbon, that is they have V,H and R. (Its the middle two)

It was Bob Burn who first told me about frieze symmetries. He often wrote about them in the ATM journals. For example, he gave Logo instructions to generate them in Micromaths (Spring 1995).  Bob was a dedicated scholar of mathematics education who worked at Homerton College. This was before it became a college of Cambridge University, and when it specialised in teacher training for undergraduates and postgraduates.  He later moved to Exeter University and was influential in thinking about the pedagogy of undergraduate mathematics education. At Homerton I taught several courses for teachers that Bob had helped design, and they always had two features.

First, they were advanced mathematics courses – but the mathematics included was the kind that underpinned the school curriculum. Teachers learnt about number systems, geometry and symmetry, how to categorise change and identify structures that stayed invariant, how to justify their reasoning and what was considered mathematically beautiful in those fields. It was not the same mathematics as in the school curriculum but it was intended to be the mathematics that would help teachers later, when they or their pupils raised questions about maths. (Now I realise we should have set up a research project to investigate this claim!) This is not a new idea: Felix Klein’s work in mathematics education before 1910 was titled ‘Elementary Mathematics from a Higher Standpoint’ and is definitely undergraduate-level mathematics.

Secondly, these courses for teachers were based on a pedagogic principle of suggesting just enough mathematics for people to start doing mathematics and asking their own questions.  I link that to the OU phrase ‘manipulate; get a sense of; articulate’.

When Bob drew the friezes he used a rather dull basic shape, like a flag, to make his motifs.  I decided to be more seasonal and see what motifs I could come up with. So that year a group of prospective mathematics teachers worked on identifying motifs and symmetries in these seven friezes:

Activity:

Which friezes have Horizontal symmetry? Vertical symmetry? Rotational symmetry? Which have more than one of these? None of these?

Can you find a motif for each frieze? Where there is a choice of motif can you find one that has exactly the same symmetries as the whole frieze?

Can you draw a motif that has V and R symmetries but not H?

One of the reasons I like this activity is that it creates – in me at least – a need for some new mathematics.   While I can ‘see’ horizontal and vertical symmetry (unlike some students) it always takes me a bit of time to appreciate rotational symmetry.  It helps to try and draw my own motifs.

I can also see that the reindeer pattern has some sort of symmetry, but it is not one of the ones that I know about – not H, V or R.  It’s the same kind of symmetry that makes my oak leaf ribbon beautiful, a horizontal reflection that is slightly out of step. Because I had noticed something and needed a name for it, I was delighted when Bob told me about the new bit of mathematics I needed: a glide reflection. First you reflect then you translate (glide) parallel to the reflection line.

The glide reflection G must fit perfectly with the basic repeat translation. The basic motif includes two reindeer, one facing up and one facing down, and I need to translate it through its full width for a pattern repeat. But if I do a glide reflection with the ‘glide’ part being exactly half the length of the motif, then it lands perfectly on itself, leaving the pattern invariant.  So this frieze has a glide reflection G and it has the basic symmetry T, but it does not have H or V or R.

The symmetry in the oak leaf ribbon is also a glide reflection: each leaf is reflected to the other side of the ribbon and moved down by 1.5cm, which is half the pattern repeat. There is also one in the frieze of angels, but that is not the only symmetry there. Once alerted to the existence of glide reflections, you will find you see them quite often. It’s a very attractive design feature, with a lovely sense of direction: a bit like footprints. I challenge you to find it in other decorations.

Last thought and activity: There’s a lot about friezes on the internet, usually pointing out that there are seven frieze groups. So: why seven? And particularly, why only seven?  It’s been easy to find friezes with no symmetry apart from T, and ones with just H, just V, just R, just G – that’s five types without even trying. But what about patterns that have H and V, G and R, … or three of these … or even all four? That is the kind of question about mathematical reasoning that I (and I guess Bob Burn) would want teachers to ask and encourage.

Activity

Can you prove that there are only seven distinct types of frieze? 

One approach is to consider all the systematic variations; try to draw an appropriate motif for each one, and see what happens. 

Bob’s articles in the ATM journals show some ways of constructing these motifs with flags although I prefer the creativity of finding images and playing with them in computer  ‘art’ or geometry packages.   Of course he gives no answers, because the point is to enjoy working it out. (If you can access a university library, there is an article by Belcastro and Hull that does). 

References

Belcastro, S.-M., & Hull, T. C. (2002). Classifying Frieze Patterns without Using Groups. The College Mathematics Journal, 33(2), 93–98.

Burn, R. (1995) Friezes with Logo. Micromaths 11:7-8.

Burn, R. (2008) Friezes. Mathematics Teaching 211:21.

Klein, F. (1908, 2016). Elementary Mathematics from a Higher Standpoint. Berlin, Heidelberg: Springer Berlin Heidelberg.

This weekend I was invited to Bletchley Park to run a code breaking workshop with a group of year 9 students, as part of our Open University and Royal Institution mathematics masterclass series.

It also happened to be the Park’s 1940’s vintage weekend so, as I arrived I was greeted by soldiers in world war two uniforms, guarding the front entrance.

Inside the world heritage site, staff and visitors alike were dressed to impress in 1940’s attire. Vintage vehicles, including an army jeep, Spitfire and tank, were proudly displayed around the grounds, guests played lawn games and swing music blasted out of a wireless radio, creating a nostalgic atmosphere.

Staff and visitors dressed in 1940s clothing for the vintage weekend

Of course, in the 1940’s, when Bletchley Park was in full operation, it was not all fun and games.

During the Second World War, Bletchley Park was home to the Government Code and Cypher School and it was the job of mathematicians working there, including Alan Turing, Joan Clarke and Bill Tutte, to decipher intercepted military communications sent by the Axis nations. These included messages encoded with the German Enigma and Lorenz ciphers, which cryptanalysts had thought unbreakable.

Building on a breakthrough made by Polish codebreakers in Warsaw, Alan Turing and Gordon Welchman designed an electro-mechanical machine, known as the Bombe, to rapidly decode and transcribe Enigma encoded messages. Colossus, the world’s first programmable digital computer, was also used at Bletchley Park to decipher high level messages sent using the Lorenz cipher.

This work provided vital intelligence in support of Allied military operations and is credited with shortening the war by two years.

Working at the Open University, just a few miles down the road from Bletchley Park, it is hard not to feel inspired by the men and women who worked there. So when I was asked to run a workshop within these historic grounds, I jumped at the opportunity and a cryptography challenge seemed the obvious choice for my session.

A code breaking masterclass – the cipher challenge competition

After successfully getting past the military police at the identity card check point, I headed over to Block B, home to ‘The Life and Works of Alan Turing’ gallery and the coding centre’s Education Department, where our masterclass series takes place. I was joined by Sue Pawley from the Open University, who organised the series, and Tom Briggs, Bletchley Park’s Education manager.

The Education Department in Block B

This particular masterclass was set up as a competition, with twelve quick fire rounds, designed to create a sense of urgency, build tension and encourage strategic team work. In this way the students could begin to empathise with the code breakers of Bletchley Park and understand the immense pressure they were under during the war.

Students worked in small groups to decipher secret messages, working against the clock to crack the codes and get the decoded messages back to the base, before the other teams. They learned how to encode and decode messages using a range of classic codes and ciphers, including substitution ciphers such as the Pigpen (or Freemasons), Caesar and Hebrew “Atbash” cipher, and transposition ciphers like the Scytale and Rail-fence. There was also a bonus round, which involved deciphering numbers sentences, for example: 64 S on a C B and 32 is the T in D F at which W F (answer at the end*), for students to work on between rounds.

Working on the Bonus round, with a little help from Bletchley Park’s Tom Briggs

One of the oldest ciphers the students worked with, was the “Scytale” transposition cipher, used by the Spartans in Ancient Greece. In the 3rd century BC, a parchment would be wound around a cylinder, before a message was written and the unravelled parchment was sent to the intended recipient. For the students, this meant wrapping the cipher-text around a pencil to unscramble the letters and reveal the original plaintext.

The “decoders” working on the Scytale cipher using a pencil

One team of students worked out that they could solve this cipher without using a pencil, by simply ‘jumping’ along every six letters, deciding that this method was more mathematical. Unfortunately it was also a much slower method, but I was pleased that they had spotted this pattern and if they were decoding a longer message, this generalisation would have been helpful.

A Spartan “Scytale cipher”

The most famous mono-alphabetic substitution cipher, the Caesar cipher, was required for the next quick-fire round. Students solved this challenge by setting their Caesar wheels to a shift of 3, since this was the way historians believe Julius Caesar used this cipher when sending messages of military importance.

Team “cheese crackers” deciphering a message using a Caesar wheel

As the Caesar cipher is very simple, swapping one letter for another, it is a weak code that is easy to crack. As a group, the students discussed how to make this cipher stronger. This included a suggestion to “jumble up” the letters in the cipher-text strip so they were not in alphabetic order. This lead to a bonus challenge question: in how many different ways can the letters of the English alphabet be rearranged? The students produced a range of answers, including a sensible but incorrect suggestions of 26×26, but two teams were able to identify the solution: 26! (or 403 291 461 126 605 635 584 000 000). One team was able to correctly name an approximation of this number as four hundred septillion.

Trying different shifts using a Caesar cipher wheel

Modern cryptography is most often used to provide confidentiality and security when sending sensitive information, including bank details, via computers, so it was important to look at binary encryption. Some of the students had met the binary number system before, but for most the name was a familiar but scary and unknown concept. One student was able to explain the use of ones and zeroes to mean ‘on’ and ‘off’ functions within computers. Another student was able to explain that the ones and zeroes represented powers of 2, starting with 2^o, i.e. 1, and that the equivalent decimal (or denary) number was equal to the sum of these values.

The “codebreakers” converting numbers from binary to denary to decode a message

When computers send information, usually in binary form, elements of the message can sometimes get changed in error during transmission. For this reason, data needs to be checked for corruption. In the next part of the session the students looked at how data can be “error checked” using a two-dimensional parity check.

This particular method works by adding an extra row and column of values to the original data which each act as a label. In the example below, 1 is added to the end of a row or column if there is an odd number of 1’s and a 0 is added for an even number of 1’s. In other words, the final value in each row or column contains the sum of that row or column, modulo 2.

Example of how to find an error using the two-dimensional parity check method

This challenge was set as a relay-race so that students had to find the error in each set of data before being given the next. This round required speed but students learnt that accuracy was ultimately more important as those teams who rushed and made mistakes were sent back, losing valuable seconds.

The “error-checking” relay challenge was a close round!

There is a useful video about parity checking here. You can also visit the National Museum of Computing, within the grounds of Bletchley Park, to find out more about binary and error checking.

The final!

During WW2, Alan Turing and the Hut 8 team used a combination of educated guess work and clues, including knowledge about where the message was intercepted, to decipher German military messages. Up to this point in the competition, the students had been told about the cipher used in each round and were given some information about the key, ultimately making the process of deciphering relatively straightforward. Of course, in any real code-breaking situation, where you are not the intended recipient of the message, you are not going to know the cipher key.

In the final and deciding round, the students had to use clues, including a bar chart depicting the frequency analysis of letters in the English alphabet, to decode one last message, getting a sense of the difficulty faced by the Bletchley Park code breakers.

The most common two and three letter words in the English language

This was a challenging task since many students struggled with the ambiguity that this method created. Assumptions had to be made and a trial and improvement approach was required. More than anything, students needed to use logic and their common sense in this round, to place likely words and adapt their solution as it developed.

“Team one” solved the frequency analysis round in record time!

It was a close call between the top three teams, but the final result meant team “JABLE” (named from the initials of the team members) were victorious, leaving Bletchley Park as Code-breaking Champions.

What struck me about this session was that the students naturally engaged with and discussed, problem solving strategies. Teams divided up the challenges and allocated roles in order to collaboratively decipher messages, quickly and accurately. Students used their natural mathematical powers to look for generalities within sequences and conjectured about solutions that made sense within the context. I was particularly impressed by the resilience that the students demonstrated when faced with unknown problems and when they became “stuck”. The history behind this mathematical masterclass seemed to give these students a common goal and a sense of working towards something greater.

Andrew Wiles, the mathematician who famously proved Fermat’s last theorem, recently said that “accepting the state of being stuck” is the essence of being a successful mathematician. Like the Enigma code, which was thought to be impossible to decipher, Fermat’s last theorem was long thought to be impossible to prove. What Turing and Wiles had in common when working on these “impossible” problems, was the resilience and perseverance that prevented them from giving up.

According to Tom Briggs, the Allies strengths, which ultimately lead to cracking the Enigma code, were: luck, inventiveness, bravery, persistence and secrecy. The students certainly showed inventiveness and persistence, and I am sure the winning team would argue that luck that nothing to do with it!

Find out more about Royal Institution mathematics masterclasses

The Open University is responsible for organising four Royal Institution secondary mathematics masterclass series held at: Bletchley Park, the Museum of Science and Industry in Manchester, the University of Bradford and the University of Worcester.

For six weeks, children in year 9 from local schools are invited to participate in exciting mathematical workshops, such as: Games, Goats and Gold and Infinity: Friend or Foe? The aim of the series is to stimulate and encourage young people in the art and practice of mathematics, to develop a sense of enjoyment in the subject.

If you want to send some students along, you can find out more about these series here: http://mcs.open.ac.uk/RI_MasterClasses/.

If you are interested in delivering a workshop or volunteering to support a session for the 2018 series, please get in touch: [email protected].

For more information about the Royal Institution Mathematics Masterclasses national programme, which also includes masterclasses for primary-aged children, see: http://www.rigb.org/maths.

Visiting Bletchley Park and The National Museum of Computing

If you have not yet visited Bletchley Park, no longer the world’s best kept secret, it is definitely worth making the trip!

A view of the mansion from across the lake. 

I recommend signing up for a free guided tour of the Park and attending one of the Enigma and Turing Bombe live demonstrations.

If you have time, you should also include a trip to the National Museum of Computing to see the magnificent Colossus rebuild.

More codes and Ciphers

If you are interested in finding more about codes and ciphers or are looking for resources to use with your classes, these websites offer some fantastic ideas:

• Crypto corner
• Black chamber
• School code breaking

*Answers

64 squares on a chessboard

32 is the temperature in degrees Fahrenheit at which water freezes

I’m Sue Forsythe, the latest member to join the Mathematics Education team at the Open University. I have worked in Mathematics Education all my career, first as a secondary school teacher of Mathematics and latterly as an Initial Teacher Educator of Secondary Mathematics. I understand the need for Mathematics to be taught by teachers who have a deep understanding of mathematical concepts and a secure pedagogy to be able to develop these concepts in their students. The Smith review recommends the near universal participation of 16-18 year olds to continue studying Mathematics. As a result there will need to be increased capacity in the teaching profession to deliver this. The OU Honours degree in Mathematics and its Learning has huge potential to develop this capacity, both within students taking the whole degree and with specific modules available for those teachers in schools and colleges who change to specialise in teaching Mathematics.

My doctoral thesis, completed in 2014, used a Design Based Research methodology to explore whether a task in a Dynamic Geometry Environment could be the catalyst for the development of the concept of inclusion in 2D geometry in 13 year old students. The research allowed me to make a fine grained study of how children think about shapes and develop understanding of important mathematical concepts such as inclusivity. One important finding from the study was the affordances of the dynamic figure at the heart of the task which includes the facilitating of a narrative through which students can construct meanings. This makes reasoning in a dynamic environment qualitatively different from reasoning in a static (pencil and paper) environment. Generally, how learners reason in a dynamic environment could be an immensely fruitful area of research to help us understand how best to create effective online learning.

This lends itself very obviously to the learning of mathematics online which should be more than simply an electronic workbook, even if the computer provides instant feedback. I believe that further research is needed in how to make the most of the affordances of interactive maths software.

Cathy Smith and Charlotte Webb discuss the Open University and Adrian Smith’s Review of post-16 Mathematics

Charlotte:
Cathy – you have recently joined the Open University team. Welcome. Tell me a bit about your experience and interests in mathematics education.

Cathy:
Well, I have recently come from a big mathematics education team at UCL Institute of Education. I have been working in mathematics teacher training and professional development. I am really pleased to be taking that work forward here in Mathematics Education.
My research interests are in two areas. One that I am very passionate about is the participation of young women in mathematics. I have researched adolescents at the stage of them choosing whether or not to continue with mathematics, looking at how they are positioned by wider discourses about what it is to be a girl or a boy, and how it feels to be at the intersection of multiple identities: mathematics student, hard worker, friend, son, daughter. One of the reasons the Open University has always appealed to me – and I have been an associate lecturer in the past – is the chance it offers for people to come back to studying, and specifically to come back to mathematics.
The other area that I have recently been working on is designing courses for beginner teachers to prepare to teach A-level mathematics. This has been a project with the Further Mathematics Support Programme. Our research suggested that new teachers get limited experience of teaching level 3 mathematics during their training – because they are rightly concerned with other aspects of classroom and curriculum management. So over the last three years we have rolled out online and face-to-face courses in which beginner teachers can enrol to look at aspects of A-level mathematical knowledge from the learners’ and teacher’s points of view, combining learning about subject and pedagogy. I think this also is fit with the Open University aim to offer opportunities for teachers and others to upskill themselves in mathematics, maybe consolidating their knowledge, maybe looking to teach a wider range of content or students.

Charlotte:
Yes, exactly. We have over 1000 students every year enrolling on our core mathematics module. About ten percent are on the mathematics education pathway and many others tell us they intend to teach.  For example one of our students, Joanne Breeze, is studying in Wales for the BSc in Mathematics with a view to becoming a teacher. She was originally an electrical engineer, after first going off to a red brick university, then following an apprenticeship route instead. She returned to study and decided to retrain after having children. Lots of our students have similar stories and are returning to formal mathematics study after time in the workplace. Then, others come to us because they prefer flexible, distance-learning options that we offer. Many are already working in schools in support roles, so we are aware that schools want more mathematics specialists who can also communicate and work with children.
 
Cathy:
Adrian’s Smith report has just been published setting out the future needs for post-16 mathematics. He has recommended that, in the longer term – about ten years – the government should expect every 16-year old to be studying some mathematics. I think he makes a very good case that employers want graduates with some quantitative skills, whereas many of our 23-year old graduates have not studied any maths for five years. It is not only teachers who have to pass a numeracy test.

Charlotte:
As a country we need mathematical skills for people in STEM jobs – but also in non-STEM jobs because these are becoming increasingly data–driven. I recently heard the film animator Sydney Padua talk about the importance of using mathematical tools in her creative work.

Cathy:
I agree with universal participation as a goal but it is difficult to see how that could be compulsory. I think we need a range of pathways so that every 16-year-old can see a choice that offers suitable mathematics for them, whether that’s functional maths, vocational maths, Core Maths, A-level etc.  I once did a review of the curricula in high-performing jurisdictions, and they all had a range of pathways post-16 that included maths for work, maths and statistics as well as a calculus route like A-level.  Then of course there is the question of the teacher workforce required …

Charlotte:
…which will only add to the increasing recruitment demands for specialist mathematics teachers, and they will now need to be effective in teaching that range of courses.  Adrian Smith recommends investment in continued professional development in mathematics for teachers of post-16.

Cathy:
Yes, and if all these teachers are needed post-16, this may have a knock-on effect and mean that schools would find it hard to provide specialist teachers for the new GCSE, or for GCSE resits in FE. Realistically there is going to be a huge need to bring new entrants into the profession or for teachers from other subjects to retrain in mathematics.  And that where we have to say the OU can help.

Charlotte:
Our mathematics education modules were originally designed for improving teachers’ knowledge of mathematics, and how mathematical thinking develops. We have got reach across the four nations, and in fact we have already been working with the Irish government. We have matched up our maths modules with the new standards that they require from specialist teachers. So teachers can learn at a distance, while they work.

Cathy:
What I see as the next stage for mathematics education in the Open University is to make our modules more accessible for people in schools or any other busy work environment. You might not need a full second degree, but as an educator you do need to understand how the school mathematics curriculum prepares students for the next stages of study. You need to know how to analyse the data sets that students meet at GCSE and A-level, and how mathematics helps us model movement and forces. Explaining how mathematics is applied in biology, or how it has developed historically through human problem solving, inspires students to learn more and to keep participating in maths. So at the OU, perhaps that means presenting the best tasks, and the most relevant content, in more flexible units. There are some great, short professional development courses around but they don’t offer the breadth and support of an OU undergraduate module. So in the next few months I will be thinking about what we can offer as professional qualifications for existing teachers and new ones. And how this can make use of our expertise in teaching enabled by technology. And crucially talking to schools and Maths Hubs about their priorities for developing and retaining mathematically skilled teachers. The OU wants to make changes, and this fits well with its vision of becoming more agile and engaged with employers.