This blog post was written by Ann Jehan, an ME627 student who received the 2018 Open University Stanley Collings prize.

The Stanley Collings prize is awarded annually by the School of Mathematics and Statistics. The prize is awarded to the student whose Mathematics Education assignment best combines innovation in devising materials suitable for learners and insightful analysis of their learning.
The prize panel said “Ann’s learning design included a sequence of thought-provoking activities that combined open exploration and probing mathematical questions.”

Developing Geometric Thinking was the last of the four modules that I studied for the Graduate Diploma in Mathematics Education over a two-year period. I embarked on developing geometric thinking believing it would be one of the less challenging modules for me. I enjoyed geometry at school but hadn’t returned to it in any depth since then. I enjoy working visually and having had a previous career in illustrated publishing I really thought I was a visual person. Almost immediately I found this challenged; I had never been asked explicitly before to imagine a shape and manipulate it mentally. I couldn’t even see a square, let alone change it in some way. It was a complete revelation to me that other people could summon up a perfect image to order. I don’t have any internal imagery it would seem (though I do dream); rather I must think of shapes as a concept as I just don’t ‘see’ them. Frustrating, but interesting to know that I am not alone.
Unable to generate images to manipulate myself, I found using the software Geogebra particularly useful in exploring geometric ideas during this module. With this in mind, both my End of Module assignment tasks made use of its dynamic nature, to create images and allow my learner to manipulate them to test geometrical relationships. Following is an excerpt from my assignment describing one of these tasks. The learner was asked to investigate the properties of a parallelogram, by exploring the shape, (measuring sides and angles etc.) and making conjectures about which properties are invariant to all parallelograms. I chose this task because I like challenging learner’s misconceptions. As this learner was an adult, I was hoping for a particularly engrained idea of what a parallelogram is. It is always interesting when a long-held misconception gets highlighted. I know this all too well having made a fundamental error earlier in the module with the sum of internal angles of a pentagon. I know that it is 540°, but in my mind, 360° represents the ‘whole’ – an obviously deeply engrained and fixed idea left over from working predominately with quadrilaterals and circles in my school days.
Planning the task for my learner
My learner is a woman in her 40’s who works as an orthoptist. Whilst she uses angles as part of her diagnostic tools, she hasn’t had any exposure to formal geometry since school. I chose the task “Properties of a Parallelogram” to give her the opportunity to develop her mathematical powers of Conjecturing and Convincing (Johnston-Wilder and Mason, 2005). Everything she hypothesises will be just that, a conjecture, until she can convince herself that something is true. To support her in engaging these powers, I plan to use the pedagogic construct Structure of Attention (Johnston-Wilder and Mason, 2005). I want this learner to change her focus, shifting awareness from the outwardly simple nature of the tasks to discerning the underlying details. These details will be the start of her conjectures, and the process of convincing herself will help develop her geometrical thinking.

Figure 1: Properties of a parallelogram task

Figure 2: Module bookmark showing the key module ideas for Developing Geometric Thinking
To help her use her initiative, I will have a page of prompts borrowed from Watson & Mason (1998) (figure 3). I want to avoid the didactic tension described by Brousseau (1984), particularly with the parallelograms. It would be all too easy to guide her to the properties I want her to find. The more specific I am in signalling the results I want from her, the less likely it is she will have opportunity to exercise her powers of conjecture and convincing.

Figure 3: Prompts
With task “properties of a parallelogram” I plan to ask her to draw a four-sided shape, she has the freedom to draw anything she wants, but constrained by the number of sides. I will then constrain it further until eventually she can only draw a parallelogram. Along the way, we will have highlighted the properties she can see in her shapes. This mathematical theme of Freedom and Constraint (Johnston-Wilder and Mason, 2005) will allow me to access her sense of geometrical awareness before we move onto Geogebra. Using the properties found we will reconstruct one on the geometry software so she can use the tools to make reasoned conjectures about properties for all parallelograms. The dynamic nature of the software will allow her to drag a corner and see the shape adjust before her eyes and give her the opportunity to experience the power of specialising. She hasn’t used Geogebra before, so I am anticipating doing the constructing and then letting her have controls of the tools.
Observing my learner
The first shape my learner drew was a square, which is often the prototypical four -sided shape that springs to mind. I asked her then to draw a different shape but still with parallel lines, and she drew a kite, before realising that was incorrect. She then drew a rhombus and then a parallelogram.
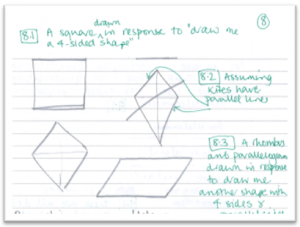
Figure 4: the learner’s four-sided shapes
When I asked her to name the parallelogram she correctly identified it, summarising the properties as two pairs of equal parallel lines. Asking her what she meant by ‘equal’, she clarified, ‘equal in length but also parallel’. Here her structure of attention is shifting from the whole, to starting to see it not only as a set of properties, but also how they relate to each other.
Moving to Geogebra, I constructed the parallelogram in front of her as planned, ensuring she felt we had included these properties. With a quick look around the tools of Geogebra she was keen to be very hands on. After making initial (accurate) conjectures about the internal and external angles, she was able to convince herself that they held true for all parallelograms by utilising the dynamic nature of the software and dragging different sides and vertices (figure 5). She rationalised it to herself that it was the invariant relationship of the parallel lines that ensured the angles summing to 180°.
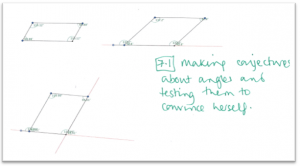
Figure 5: using Geogebra
At my suggestion we looked at the angles of intersection formed by the diagonals. The learner then identified two congruent triangles, formed from two sets of scalene triangles (figure 6).

Figure 6: Learner conjectures that parallelograms must be constructed from scalene triangles
This finding was key to preventing her seeing other quadrilaterals as parallelograms later on in the session. Again, she was convinced as she was able to move the shapes around and the angles changed accordingly but retained the invariant relationships she had conjectured.

Figure 7: My learner’s conjectures of the properties of a parallelogram
Summarising the properties, I asked her to consider whether a square, rectangle or rhombus could be a parallelogram. She was adamant they couldn’t because the internal triangles weren’t scalene, and 90° angles didn’t fit with her mental figural image of a parallelogram. She saw parallelograms as slanting because that is they have always been presented to her, a figural concept, as coined by Fischbein (1993) that had taken on an unintended characteristic for the shape.

Figure 8: This learner’s reasoning as to why squares and rectangles are not parallelogram.
Needing to challenge her convictions, I encouraged her to create a parallelogram with isosceles triangles – if she could, then this property couldn’t hold. This wasn’t something I had prepared for, so was a challenge for both of us. Her first attempt was with equilateral triangles, which made a rhombus.
She dismissed that as a parallelogram since the sides were equal. The second parallelogram had a pair of isosceles triangles, thus finding a counterexample to disprove her conjecture (figure 9). (We ended up drawing the triangles first, reversing the construction. This pedagogic strategy Turning a doing into an undoing (Johnston-Wilder and Mason, 2005) was very useful to reinforce that two congruent triangles form a parallelogram).
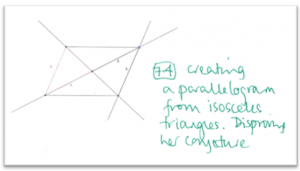
Figure 9: The learner has found a counterexample to challenge her conjecture.
Whilst shifting the focus of her attention from the whole to discerning properties definitely supported her powers of conjecture and convincing, evident also was the mathematical theme of Extending and Restricting (Johnston-Wilder and Mason, 2005). Reasoning purely on the basis of the properties she found, the learner found it very difficult to include the other quadrilaterals as special cases of parallelograms. Accepting that squares, rectangles and rhombi do actually satisfy the requirements to be included as parallelograms, required her to relax her understanding of the properties.
She also found it difficult to see squares as rectangles. The specific qualities that the learner was attending to, and allowing her to classify shapes as parallelograms, were originally too restrictive. For example, ‘2 angles on the bottom line = 180°’ (she initially restricted that to all angles other than 90°, and ‘2 sets of lines which are equal lengths’ (figure 5) couldn’t include 4 lines of equal length). It took lots of prompts to shift her focus of attention and extend the meaning of these so that squares etc. could be included.
In doing this, she also extended and redefined the meaning of the word ‘parallelogram’ to her (figure 10). Not only is it the shape she holds in her mind’s eye but is also a list of properties to which squares etc. satisfy.
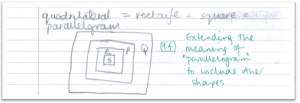
Figure 10: Redefining her understanding of quadrilateral shapes
This cycle of conjecturing, seeking a convincing solution, modifying or refining her conjectures until she was satisfied may well have been a new way of working for her but of course it could have been the use of Geogebra that made her hesitant. Asking her to reflect on the use of the ICT she commented that having the access to creating many diagrams, quickly, being able to correct as necessary, really helped her to work in an exploratory way, which of course was key to convincing herself of her conjectures. It also supported the theme of Freedom and Constraint. She had the freedom to create any different parallelogram by dragging vertices and edges but constrained by the way I had constructed it. Parallel equal sides remained invariant whatever she changed. On reflection though I wonder if I could have given this learner more responsibility to create her own from scratch, to fully ensure she appreciated the underlying construction and relationships in the parallelogram. In this sense the freedom she had was a fallacy.
I’ve really enjoyed the work I did with these four Mathematics Education modules and the opportunity they gave me to really reflect on my learners’ mathematical thinking and indeed on my own. Recognizing when I or my learners are using a concept from the modules (see figure 2 for those in ME627 Developing Geometric Thinking) has been very satisfying and ensures that I work harder to provide opportunities for learners to enhance their mathematical thinking. I hope that this will lead to a deeper understanding of why and how the maths is, with learners becoming more confident and willing to take the initiative with their learning.
References
Brousseau, G. (1984) The crucial role of the didactical contract in the analysis and construction of situations in teaching and learning mathematics. In Steiner, H. (ed.), Theory of Mathematics Education, Paper 54. Institut fur Didaktik der Mathematik der Universitat Bielefeld, pp. 110-19.
Fischbein, E. (1993) “The Theory of Figural Concepts.” Educational Studies in Mathematics, vol. 24, no. 2, 1993, pp. 139–162. Available from: JSTOR, JSTOR, www.jstor.org/stable/3482943. (Accessed 13/2/18)
Johnston-Wilder, S. and Mason, J. eds., 2005. Developing thinking in geometry. Sage.
Watson, A. and Mason, J. (1998) Questions and Prompts for Mathematical Thinking. Derby: Association of Teachers of Mathematics.’
