This post was written by Nazanin Nikanjam, a mathematics education student who received the 2019 Open University Stanley Collings prize for her writing.
I have been teaching Mathematics and English as an Additional Language for the past 26 years, with the last 14 in schools offering the International Baccalaureate Programmes in London, UK and Bologna, Italy. When I was at university studying Electrical Engineering in the early 90s, I started a part-time job as a teacher. I fell in love with it and have remained in teaching ever since. I believe Mathematics is often taught in a way that discourages learners to think critically, and I have always been interested in creating resources and engaging my learners in developing a deeper understanding and appreciation for this subject. However, it wasn’t until I came across the two Mathematics Education modules ME620 and ME627 during my studies at the Open University (for the BSc in Mathematics and its Learning) that I was able to understand and analyse my own thought process and transfer this learning to my classroom. Also, prior to studying the ME627 module (Developing Thinking in Geometry), I had used GeoGebra only as a graphing tool, and was not familiar with its many other applications. I was quite excited to learn how to use other features of GeoGebra to enhance my learners’ experiences and facilitate their mathematical thinking. This is why I decided to use it in my End of Module Assignment task.
The plan
I worked with a group of 15 year-old learners for this task, the majority of whom had a fair understanding of shape and measure, but had mostly been practising algorithmically with a lot of repetition and substituting in formulae (e.g. to find the area of a composite shape). My interest in working with this group of students came from the fact that they had not previously been exposed to tasks that require higher order thinking. My aim was to engage them in seeing beyond the obvious.
I chose to focus on 3 learners who had very different approaches. I was curious as to how their different ways of thinking would influence one another. I planned to provide these leaners with one task that emphasized analysis, and the other synthesis. I chose task 4.4.2 (Sliding ladder) from the book Developing Thinking in Geometry (Johnston-Wilder and Mason, 2005), where learners are asked to make a conjecture about the path a ladder’s midpoint traces as it slips from the wall to the ground. I anticipated that my learners would be encouraged to use their powers to analyse (both the parts and the whole) throughout this task. For my second task I chose An Unusual Shape, an exercise I found on the nrich website at https://nrich.maths.org/2161. This task I believe calls for synthesis as it requires learners to bring together their understanding of several different concepts.
For the first task, I planned to extend it by asking my learners to explore what path any point on the ladder will trace out as it falls. I also created the stimulus on Geogebra for them. The aim was to facilitate the learners’ thinking and get them to move between at least two of Enactive-Iconic-symbolic modes (Johnston-Wilder and Mason, 2005).
I planned to start the second task by providing the diagram first without the instructions and asking the learners what they may be asked. I anticipated that this would encourage them to use their powers to ‘see’ connections, and ideas come to their attention organically and through sense-making. After this I would give them the instructions and the freedom to choose how they would like to approach it. I would scaffold their thinking by giving them prompts in the form of questions that would encourage reflection, such as ‘What else can you see?’ or ‘How do you know?’
Finally, I expected that Geogebra could help them visualize the different paths in the Sliding Ladders problem, so that they can make better sense of what was happening. I also expected that it would motivate my learners and allow them to focus on dimensions of possible variation by drawing their attention to what is changing and what is staying the same.
The experience
At the start of the Sliding Ladders problem, the learners were presented with a slide containing the task instructions that appeared one at a time. The first step was for them to discuss their thoughts. Two learners agreed that “the mid-point will trace out a straight line perpendicular to the ground”. The third learner suggested that “it will curve down … like a slide, in and out”. After a short discussion they each drew a diagram and then shared their thoughts again. They chose to start with a 5-meter long ladder (specialize) and each made a different generalization.

Image 1 – task instructions for 4.2.2
It was clear to me that they were finding it easier to have the diagram to manipulate (iconic mode). One of them made a conjecture (and sounded very excited) that “it’s a circle! And it’s radius is half of the ladder!”
When they started using GeoGebra, there was a clear shift in how Learner 1 was engaging with the task, from being quite passive to seeming motivated, which emphasizes the importance of providing the opportunities for a variety of preferences. Using GeoGebra helped them explore the path for other points.
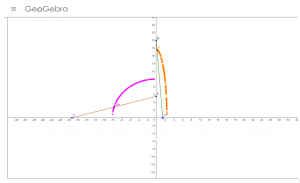
Image 2 – screenshot of the GeoGebra worksheet
They made a conjecture that “the path is an ellipse, except for the mid-point that follows a circle”. Learner 3 was the only learner who then moved to symbolic mode in recording her thoughts and tried to verify the conjecture for the mid-point “I’m going to find a rule”.
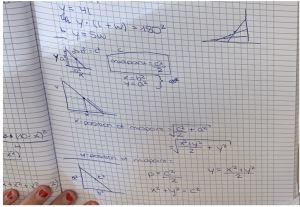
Image 3 – learner 3 using symbols to record the conjecture
We ended this task after a discussion in response to one learners’ question: “What happens if the ladder is not straight?”
In the second task the diagram was the only item on the board at first and then the rest of the instructions appeared one at a time. My first question with only the diagram on the board was “What do you think you may be asked about this diagram?” One learner responded: “how many trees can you plant in the light green?” and another one said: “find the area of the cut grass”. After displaying the instructions, the group started to discuss their approach and moved on with drawing their own diagram and dividing it into sections.

Image 4 – task instructions for An Unusual Shape
As learner 1 was finding it difficult to visualize the rope, I offered him a piece of string (enactive mode) which he started to manipulate and make sense of the now sectioned diagram.

Image 5 – the learners working on their own diagrams
Once they were convinced that they had found the answer to questions 1 and 2, learner 2 attempted to answer question 3 through trial and error, and learner 3 conjectured that “it will be a larger area if the rope was tied to a point in the middle of the shorter side”. She was excited about this conjecture and went to the board to explain her reasoning to everyone in the class: “Look! If you split the 10 ft side by two and tie the rope there, you’ll get the largest area!”
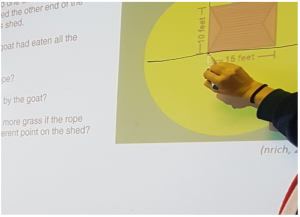
Image 6 – the learner explaining her conjecture on the board
Before question 4 was displayed, the group were already discussing it: “is there a point that gives an even bigger area?” They decided to think of the distance at which the rope is tied on the 15ft side of the shed and work out the area from there. Answering this question proved to be a challenge for them, so once they had an algebraic expression, they decided to use Google Sheets to conjecture: “It has to be tied to the corners!”
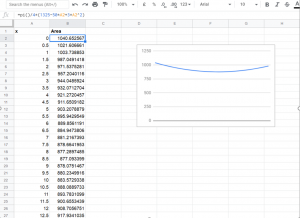
Image 7 – deducted formula used to calculate the area on Google Sheets
The final question sparked a very interesting discussion about a possible application of this task being for a gardener to find out where to install a sprinkler system, or the best position of a router in a building with an obstruction.
Reflection
My learners’ response to both tasks was positive with instances of surprise, engagement and a final sense of accomplishment. When leaving the classroom, a few learners exclaimed “I liked this!”, and this was my biggest reward. I believe there are a few factors that contributed to the success of this exercise. Firstly, the open-ended nature of these tasks and the opportunities to ‘discover’ enabled the learners to exercise their powers. They were encouraged to imagine and express their thoughts at the start of the first task, and the possibilities of what there is to be found in the second one. There were several opportunities to move from specializing, to generalizing, both to find a solution to the presented problem, and to satisfy their own curiosity and assumptions (e.g. “Is there a point that gives an even bigger area?”). They had opportunities to make conjectures (there was enough challenge to invoke their curiosity, but not too much to kill their interest) and to ‘talk’ to convince each other and even the whole group with confidence. The learners were also able to recognize and use their power to organize their thoughts, to help them come to a solution (using Googlesheets).
Another contributing factor was that in planning around these tasks, I had in mind the principles that make teaching more effective (NCETM, 2007). I believe the way the students engaged with both tasks is testimony to these principles. For example, I used cooperative small groups, both tasks involved higher order questions and encouraged reasoning, and they built on the knowledge the learners already had.
The tasks were similar in how they were both open-ended (the second task with more scope than the first) and facilitated the use of a strategy known as ‘Do, Talk, Record’, which in turn helped the learners progress through them by sharing ideas and building on each other’s powers and strategic thinking and not feel disempowered by their individual absences. Both tasks led the learners to use their imagination and to ask ‘what if …’ questions and look for ‘another and another’.
Both the learners and I found the second task more interesting. I was merely an observer during this task, with very little involvement. I felt all I had to do was to throw in another question or give them a nod to continue to explore. Perhaps what they found more interesting about this task was the presence of a more tangible context and the opportunity to think of their own authentic examples.
What surprised me about the learners was the many ways in which they stepped into the problem. For example, learner 1 seemed to find it difficult to imagine without having a physical stimulus (enactive), he also seemed to be more concerned with the whole, whilst learner 2 would rely on imagery almost all the time (iconic). She used visualizing to step into the problem, model it and plan ahead (Piggott and Woodham, 2009).
Learner 3 on the other hand was keen to express her thoughts in symbolic form, and it was evident that she was making intuitive jumps. She was also more reflective on her own thinking. Observing her reminded me how easy it is to take your own powers for granted and expect everyone to ‘see’ what you see. She also needed her space to work on her own in the recording stage, and join the group for the talking and doing.
My approach to geometry and developing thinking in geometry has changed as a result of completing this module and practising the ideas and framework provided. I used to lack the awareness of how we process concepts in geometry, and the terminology and structures that can help to identify these processes. I now find it easier to approach conceptual problems, from stepping into them to thinking of other ways to find solutions. As a result, I find myself to be a much more effective facilitator to my students and how they can develop their thinking. Reflecting on my development both as a leaner and an educator, and looking back at the introduction of this module, I was able to recognize that geometry is more than our understanding of space, and is linked to our brain power and innate ability to navigate, imagine and design. However, what I was unable to recognize then, was the way tasks and activities can be designed to help learners activate their powers and develop geometric thinking. I have learnt that simple pedagogic devices, such as asking learners to express what they see, can be a powerful tool in helping their thinking. Or leaving some ambiguity so that the leaners can make decisions and engage in chains of reasoning.
I would like to end by sharing that what I enjoyed most with these tasks is how the majority of the learners in class were able to ‘own’ the problem and to be involved a lot more in ‘doing’ what was needed rather than being told what to do and how. According to Dale (cited in Anderson), the most effective methods of learning involves direct, purposeful learning experiences. These tasks, although not completely hands-on, empowered the learners to lead their own learning. My aim as a teacher is to provide as many opportunities to myself and my learners to experience meaningful tasks and hence appreciate the beauty of Geometry. These Mathematics Education modules have helped me step closer to this aim and I have thoroughly enjoyed them.
References
Anderson, H. M. Dale’s Cone of Experience, accessed at http://www.queensu.ca/teachingandlearning/modules/active/documents/Dales_Cone_of_Experience_summary.pdf
Piggott.J., and L. Woodham, 2009. Thinking Through, and By, Visualising. [Online]
accessed at: https://nrich.maths.org/6447
Johnston-Wilder, S. and Mason, J. eds., 2005. Developing thinking in geometry. Sage.Jones, K., 2002. Implications for the classroom: Research on the use of dynamic software. Micromath, 18(3), pp18-20.
NCETM, 2007. Mathematics Matters: Deriving practices from what constitutes effective learning of Mathematics. pp. 13-14. accessed at https://www.ncetm.org.uk/public/files/30091176/Mathematics+Matters+-+The+Full+Report.pdf
