LGBTQ+ History Month Open University, Source:

Each February, LGBTQ+ History Month invites us to celebrate LGBTQ+ culture, achievements, and activism. This year’s theme is Science and Innovation, encouraging us to reflect on how data, research, and critical enquiry help drive positive social change. Mathematics is central to that mission: it sharpens our reasoning, challenges assumptions, and equips us to analyse inequalities that shape people’s lives.  

You can read about the origins of LGBTQ+ history month here: LGBT+ History Month 2026 | Stonewall UK. 

LGBT+ History Month 2026 logo, Schools OUT UK.
Source: https://lgbtplushistorymonth.co.uk/lgbt-history-month-2026/

LGBTQ+ Mathematicians  

For students and colleagues in mathematics, this month is also a chance to highlight LGBTQ+ mathematicians whose work and advocacy continue to transform STEM. Here, we spotlight four figures whose contributions illuminate not only mathematical innovation, but also the importance of visibility, justice, and community. 

Alan Turing (1912–1954) 

Alan Turing (1951). Photograph by Elliott & Fry. Public domain. Source: Wikimedia Commons.

Alan Turing’s influence on modern science is hard to overstate. A founder of theoretical computer science and artificial intelligence, his wartime work on codebreaking significantly shaped the course of the Second World War. Yet despite these achievements, Turing was persecuted by the British state for his sexuality, a stark reminder that scientific brilliance flourishes best in conditions of dignity and inclusion. Today, Turing remains both an icon of mathematical innovation and a symbol of the ongoing work needed to ensure LGBTQ+ individuals can live and work openly and safely.  

You can listen to some audio recordings about Alan Turing on Open Learn, here: Alan Turing: Life and legacy | OpenLearn – Open University 

Autumn Kent  

Autumn Kent. Source: https://500queerscientists.com/autumn-kent/

Autumn Kent is a topologist whose research explores geometry, topology, and moduli of Riemann surfaces. She has published extensively and received several major awards, including a Simons Fellowship. Kent is also a pansexual trans woman and a prominent advocate for LGBTQ+ inclusion in mathematics, organising the LG&TBQ+ conference to support collaboration between LGBTQ+ mathematicians working in geometry and topology. Her work exemplifies how mathematical creativity and community activism can reinforce each other.  

The most recent LG&TBQ+ conference (LG&TBQ2) was held in 2025: LG&TBQ2: geometry, topology, and dynamics | Fields Institute for Research in Mathematical Sciences 

Ron Buckmire  

Ron Buckmire at the 2013 Joint Mathematics Meeting. Source: https://commons.wikimedia.org/wiki/File:Ron_Buckmire_at_2013_Joint_Mathematics_meeting.jpg

Ron Buckmire is an applied mathematician whose work spans numerical analysis, mathematical modelling, and mathematics education. Beyond his research, he has played a major role in LGBTQ+ advocacy within STEM. Buckmire was a founding member of Spectra, the association for LGBTQ+ mathematicians, and has long championed greater visibility and representation for historically excluded groups. His activism and academic leadership make him a central figure in contemporary LGBTQ+ mathematical communities.  

More information about the LGBTQ+ association Spectra can be found here: What we do – Spectra 

Marina Logares  

Marina Logares. Source: https://lgbtqstem.com/2020/07/10/an-interview-with-marina-logares/

Marina Logares is an algebraic geometer whose work contributes to our understanding of complex algebraic structures. She is listed among confirmed LGBTQ+ mathematicians and is recognised for her visibility as a lesbian mathematician. Her presence in the field highlights the importance of representation and the work still to be done to ensure all mathematicians feel seen and supported in their academic environments.  

You can read an interview with Marina, here: An interview with Marina Logares – LGBTQ+ STEM 

We have picked out four examples of LGBT+ mathematicians for this blog, but there are many more inspiring mathematicians and statisticians, including those posted on the 500 Queer Scientists campaign, here. This visibility campaign which publishes self-submitted bios and stories intended to boost the recognition and awareness of queer scientists, including our own Senior Lecturer in Analysis: Tacey O’Neil. If you are LGBTQIA+ and work in STEM, STEM advocacy, STEM education (or any other supporting field), you can add your voice and story to 500 Queer Scientists. 

OU academic Tacey O’Neil

Why Mathematics Belongs at the Heart of LGBT+ History Month 

Rainbow Pi symbol.
Source: https://pixabay.com/vectors/pi-math-geometry-science-numbers-5786042/

Mathematics is often seen as abstract or detached from society, but in reality, it offers powerful tools for understanding and improving our world. Mathematical thinking helps us: 

• Analyse inequalities through statistical evidence and modelling; 

• Challenge assumptions by examining patterns and structures critically; 

• Support inclusive policies through data driven decision making; 

• Innovate responsibly, ensuring technologies reflect fairness and equity. 

This year’s theme Science and Innovation, reminds us that progress depends not only on technological advances but also on the people behind them. When LGBTQ+ mathematicians can contribute openly and authentically, the entire discipline grows richer. 

LGBT+ History Month is a moment to learn from the past, recognise present contributions, and work towards a future where all students and researchers feel welcomed and valued in mathematics. 

Sources of further information and support

The LGBTQ Hub hosts a collection of free resources exploring sexuality and LGBTQ+ history across the core faculty areas within The Open University: LGBTQ Hub | OpenLearn – Open University

For OU students, you can find Open University Library resources here: LGBTQ+ | Library Services | Open University 

You can find out about the Queer, Equality and Diversity (QED) Network for Maths, here: QEDNetwork 

This post is written by Cathy Smith from the Open University. 

I started December with a new and intriguing mathematics puzzle from the excellent UK Mathematics Trust (https://ukmt.org.uk), who have been a source of consistently excellent maths problems since I started as a maths teacher. This problem was presented to a group of maths teachers and researchers with the aim of understanding what problems we want, and can reasonably be expect, 11–16-year-olds to solve.

Our group discussed:

• what are the problem solving skills secondary school student should learn?
• What contexts should they learn and use them in?
• How difficult should those problems be?
• How familiar/unfamiliar? And how many solution steps or connections are needed?

This framework of questions reminded me of work done by the Nuffield foundation fifteen years ago, analysing the difficulty of the mathematics used in science A levels (SCORE, 2012). It highlights that much mathematics is not done in the maths classroom but is used to solve problems in other subjects.  The 2025 event,  where this discussion happened, was run by Maths Horizons who are consulting widely while they develop a map of mathematical problems and associated resources that they hope will inform and support the future curriculum, classroom practice and assessment design. You can find more about them here: https://www.mathshorizons.uk/.

Here is the problem.  You might like to read it and notice your initial reactions.

I noticed several things and, because I am used to teaching on the Open University mathematics education modules, I have the habit of labelling some of these ‘noticings’ with the names of relevant module ideas.

Perceptual and discursive reasoning (PDR)

This is a module idea from Learning and Doing Geometry.  In this problem, my attention was first drawn to the shapes P, Q and R. I recognised what kind of objects were involved by using my senses – what we call perceptual noticing – and that each was made of five identical triangles. I was not yet reasoning, but I had an intuition that my reasoning would involve comparing these similar-but-different shapes.  On the other hand, my mathematical habits reminded me I must read the description in words – because it is usually discursive reasoning, using words, symbols and diagrams, that is characteristic of school maths. It took me a while to feel sure that the technical language used did not give me any extra background information than my perception had shown me.

Freedom and constraint

This module idea appears in both Learning and Doing Algebra and L&D Geometry.  I know I need to find perimeters – a constraint on the problem – but I don’t know any lengths. This is the kind of freedom that stops many learners in their tracks.  They cannot calculate so what can they do next? If they try to think, will it be a disappointing waste of effort? The mathematical resilience experts Clare Lee and Sue Johnston-Wilder suggest teachers need to be explicit about discussing the emotional side of mathematical problem solving  (Lee & Wilder-Johnston, 2017). Students develop resilience by remembering experiences of trying a non-routine strategy that was successful.

You might like to stop here and work on the problem yourself here before reading on.

My experiences reminded me that this is exactly why algebra was invented! In Learning and Doing Algebra we discuss Radford’s description of algebraic thinking (Radford, 2014) as characterised by indeterminacy, denotation and analyticity. This problem involves quantities – the triangle’s side lengths – whose values are unknown (indeterminate). On the diagrams below you can see the notation I used to represent (denote) those quantities: s for the length of a short side and L for a long side. I could then reason analytically – first of all, recognising and writing that the perimeter was the sum of the exterior lengths and then combining like terms to get a concise symbolic expression.

I noticed another freedom in that I did not know who might be tackling this problem.  We have lengths and right-angled triangles, but could I assume the students would know Pythagoras’s  theorem and be wiling to use it in a non-routine way? I decided to give myself a constraint and try and reason keeping the two variables separate.

Combining Perceptual and Discursive Reasoning

My problem has now involved me in managing unknown lengths and I have combined perceptual knowledge (the perimeter is the sum of exterior segments) with discursive knowledge (forming three similar symbolic expressions even when I don’t know their value).  I decided to annotate my diagram to show my perceptual and discursive reasoning (in brown).

In this next figure, I had organised the symbolic expressions and compared them.  I could expand my notes to claim: P must have a greater perimeter than R because P’s expression is 2s more than R’s  (and s is positive).  I expected that all my reasoning would now be discursive, similarly based on symbols.

I don’t want to spoil your enjoyment of the problem, as there are many ways to make the remaining two comparisons. What I noticed was that I could indeed decide the ascending order by using two useful facts about the side lengths and diagonal lengths of squares. This wasn’t discursive knowledge from words and symbols but sensory, spatial knowledge of comparing journeys round a square. I didn’t use the more complicated algebraic technique of reducing the expressions to one variable (e.g. by writing L = √2 s) but I did combine perceptual and discursive knowledge into one strand of reasoning to get a convincing answer.

The Royal Society’s Early years and Primary Expert panel has recently reviewed evidence on the value of spatial reasoning. They report that “teaching children to think and work spatially results in substantially improved mathematics performance” (RS ACME, 2024, p1). For this problem, I wondered whether the depth of problem solving involved in combining spatial and algebraic reasoning was perhaps of more lasting value to most students – and perhaps more authentic to their lives after school – than a purely algebraic approach.  The problem appears in the 2020 UKMT Intermediate challenge, which is designed for students up to age 16 so some will have used Pythagoras’ Theorem and others will not. I would be fascinated to know which approaches the students used.

Lee, C., & Wilder-Johnston, S. (2017). The Construct of Mathematical Resilience. In U. Xolocotzin (Ed.), Understanding Emotions in Mathematical Thinking and Learning (pp. 269–291).

Radford, L. (2014). The Progressive Development of Early Embodied Algebraic Thinking. Mathematics Education Research Journal, 26(2), 257–277.

RS ACME (2014) RS ACME Primary and early years expert panel perspective: Spatial reasoning. Available at: https://www.royalsociety.org/-/media/policy/projects/mathematics-education/expert-panel-perspective-spatial-reasoning.pdf

SCORE. (2012). Mathematics within A level Science 2010 Examinations. SCORE (Science Community Representing Education). https://www.stem.org.uk/resources/elibrary/resource/25956/mathematics-within-level-science-2010-examinations#&gid=undefined&pid=1

In this blog we are (re)introducing our fantastic Mathematics Education tutors.

Luke Bacon 

I’ve been teaching with the OU for just over four years across a range of maths and maths education modules.

I studied Pure Maths and then completed my PGCE with the OU, before working in and around schools across London and managing a series of university outreach programmes for students from disadvantaged backgrounds. I spent some time at DfE working on Higher Education policy (ask me about the student finance system!) and have worked with lots of teachers on maths-specific CPD projects, as well as teaching on a specialist STEM PGCE course.

I also work in consulting, helping to make public services (education, healthcare, and others) a little bit better for everyone, and in my ‘spare’ time I write and examine A-level Maths and Further Maths.

Rebecca Rosenberg

Hello. I have been working at the Open University since 2019, mainly on the development of the new Maths Education modules.

Before joining the Open University, I worked as a maths education publisher, and before that I worked as a secondary maths teacher in Suffolk. I’m particularly interested in the way people talk about maths – both inside and outside the classroom; how do we form questions in maths lessons? How is maths discussed in popular culture and media?

In my spare time I knit, sew, cook, garden and binge-watch American high-school tv shows.

Tom Cowan

I have been an Associate Lecturer with the OU since 2008 when I worked on the MEXR624 summer school each year in Bath.  When that ended I was lucky enough to be offered a chance to work on an earlier maths education module. I currently tutor on all the modules which we offer in the Mathematics Education suite of modules at Level 3 (ME620, ME321 and ME322) and also E209 – Developing subject knowledge for the primary years.

I completed my Master’s Degree with the OU in 2010 so remember what it was like to study at a distance and cramming in study whilst juggling other things in life.

My current full time role is a teacher in a 16-18 SEND college working with learners who sometimes find maths challenging and often need alternative ways to see what they need to do. Previous to this I was the Programme Lead of an initial teacher education programme at the University of Plymouth. I supported the education and development of new Primary teachers on the BEd and PGCE – looking after those students with a specialism in mathematics. I have been a teacher and lecturer for over 20 years and love to watch learners suddenly “get it” when they do some mathematics!

I’ve never really left education and have found my next challenge in aiming to complete my Doctorate in Education in 2026! Hopefully I’m well on my way to becoming Dr. Cowan!

When I have some spare time, I enjoy going to the theatre, supporting Liverpool FC and Widnes RLFC and work as an officer with the Boy’s Brigade which keeps me in touch with further voluntary work (I did say spare time right?)

Jeffrey Goodwin

As well as being an Associate Lecturer for ME321, I also tutor on ME620. I first worked as a tutor for the OU in the 1980s on EM235 Developing Mathematical Thinking and returned to my current role of Association Lecturer in September 2014.

I was a classroom teacher for 10 years, working in Secondary and Middle schools. I moved into the advisory service in 1980 as Head of the Hertfordshire Mathematics Centre. I worked in Initial Teacher Training and running CPD courses for teachers; being head of mathematics education at Anglia Polytechnic University. For four years from 1986, I worked for the National Curriculum Council on a curriculum development project: Primary Initiatives in Mathematics Education (PrIME). I have always had an interest in assessment and testing and in 1998 was appointed to establish and lead the Mathematics Test Development Team at the QCA. We developed the end of key stage tests and other optional tests for all three key stages. I was in this role for eight years and then moved to become Head of Research at Edexcel and then Pearson Research and Assessment. In 2010, I became an independent consultant and worked with schools on making changes, particularly engaging with Japanese Lesson Study. For four years I was the Programme Director for the King’s College London MaST course.

I have seen it as important to make a professional contribution to education. This has involved being Secretary of the Mathematical Association, a member of the Royal Society Mathematics Education Committee and Chair of the coordinating committee for Primary Mathematics Year 1988. I have also been chair of governors of a primary school.

I have two main research interests: the role that Lesson Study plays in the profession development of teachers; and, a member of the research team at the UCL Institute of Education looking at The Nature, Prevalence and Effectiveness of Strategies used to Prepare Pupils for Key Stage 2 Mathematics Tests, a project funded by the Nuffield Foundation.

Jim Thorpe

I became a mathematics teacher through the accident of joining Bill Brookes’ PGCE course: suddenly I realised that much mathematical thinking could emerge from humble beginnings, numerical or geometrical, and realised that mathematics could make a major contribution to the intellectual and social development of adolescents if they were encouraged to function as young mathematicians within what John Mason calls a ‘conjecturing atmosphere.’

I have been committed to mathematics education for a long time, in the secondary classroom and then in a variety of ways supporting the work of mathematics teachers. My current occupation is mainly tutoring in mathematics and education, mathematics, and engineering for the Open University.

I am alarmed by much of what I see under the heading of teaching mathematics but remain unrepentant in proposing something richer than the all-too-frequent ‘training’ metaphor of communicating mathematics.

Barbara Allen

My school teaching career started in 1978 in middle schools in Worcestershire where I specialised in mathematics. I developed an interest in girls’ attitudes to mathematics and that became the focus of the dissertation for my MEd. My PhD focuses on Pupils’ Perceptions of Mathematics Classrooms and I found the ways that pupils think they learn most effectively.

In 1994, I moved to the Open University as a Research Fellow and in 2000 I became the Director of the Centre for Mathematics Education. I continued as the Lead Academic for Mathematics Education until my retirement in May 2017.

I have written on a large number of OU modules from Access to Masters Level. For some reason, I always ended up writing the sections on fractions!

I am the co-author of the children’s book series The Spark Files and the writer of the children’s radio series The Mudds starring Bernard Cribbins and Mark Benton. Now available on Audible.

My main hobby has always been music. I play saxophone in two Concert Bands and in a Big Band.

Thabit Al-Murani

Hello, I am Thabit and I am an associate lecturer teaching on the ME322 course.

I have been involved in maths education for 25 years. Over this time, I have been a teacher, head of department, researcher, and more recently I started my own freelance business offering maths education consulting and specialised tutoring. My work has offered me the opportunity to live and work in several countries including the US, Sweden, Australia, Malaysia, and the UK.

I have a DPhil in Mathematics Education and my research interests are variation theory, the teaching and learning of algebra, and SEN mathematics education.

Nick Constantine

Hello everyone, I am Nick Constantine associate lecturer for the Open University, I tutor on ME620, ME321 and ME322.  I also tutor on MU123 and MST124. I have been working with the OU for 9 years but I also used to tutor on the PGCE course from 2000-2002. I have had a very mixed career. My first degree was Astronomy and Astrophysics at Newcastle University, I then joined the Royal Navy as aircrew for a little while. I left way back in 1989 and did several ‘gap’ jobs before retraining as a Mathematics teacher and PE teacher.

My teaching career followed the standard path up to Deputy Head/acting Head but I always attended many mathematics training weekends with the ATM.  I also used to attend the MEI further mathematics conference in Nottingham for a few years. I was a Head of Mathematics in a 13-19 high school in Northumberland from 1998-2004 and enjoyed the process of organising and planning activities that reflected the fundamental philosophy of the OU ME(x) modules.

I also studied for a Master’s in Education from 2000-2002, one of my dissertations was ‘conjecture and proof in the most able’ (ME822), I really enjoyed designing my own research project and had a wonderful class to try some tasks with.  For me, if you can change the language of the mathematics in the classroom from a didactic controlling language to an atmosphere of questioning, conjecturing with learners and investigating relationships then you are really at the top of your game!

I now work part time as a teacher and OU lecturer.  I also work as a running and yoga coach and operate a small business where I organise retreats and workshops for private groups in Europe and in Scotland. Other hobbies are reading, radio 6 music, cooking and doing Maths problems!

October is Black History Month. This year the theme is “Standing Firm in Power and Pride”, honouring the resilience, leadership, and cultural identity of Black communities while marking key anniversaries such as 60 years since the Race Relations Act and the death of Malcolm X.  

Black History Month.

Mathematics and Statistics are often thought of as neutral or objective subjects, but the way we teach, learn, and engage with them is shaped by our experiences, cultures, and opportunities. The act of doing mathematics is a human activity that is universal, shared, and also deeply personal. 

We recognise the limitations of our mathematics and statistics curriculum, which draws on mathematical ideas from across the globe, but is rooted in Eurocentric traditions. As we celebrate Black History Month, it is important to spotlight the extraordinary contributions of Black mathematicians: those individuals whose brilliance and perseverance have shaped not only the field of mathematics but also the course of history. 

One such trailblazer is Katherine Johnson, whose story reminds us that mathematics is not just about numbers, it’s about courage, precision, and breaking barriers. 

Katherine Johnson: The Mathematician Who Sent Us to the Moon 

Katherine Johnson working at NASA in 1966.

 (Photo credit: NASA)  

Katherine Johnson (1918–2020) was a pioneering NASA mathematician whose calculations were critical to the success of major space missions. She performed trajectory analysis for Alan Shepard’s 1961 flight, the first American in space, and famously verified the computer-generated calculations for John Glenn’s 1962 orbital flight at Glenn’s personal request. Her work also contributed to the Apollo 11 Moon landing in 1969.  

Johnson’s career spanned over three decades at NASA, where she broke racial and gender barriers in a segregated America. Her story, along with those of Dorothy Vaughan and Mary Jackson, was popularized in the book and film Hidden Figures, bringing long-overdue recognition to the Black women who helped launch the space age.  

Her legacy is not just in the missions she helped succeed, but in the inspiration she provided to generations of students, especially young Black girls, who saw in her a reflection of their own potential. 

Read more about Katherine on Open Learn here: Katherine Johnson: NASA mathematician and much-needed role model | OpenLearn – Open University 

Dr Nira Chamberlain: Modelling the Future of Mathematics 

Professor Nira Chamberlain OBE

(Photo credit: Nira Chamberlain)

While Katherine Johnson’s legacy reminds us of the power of mathematics to break barriers and reach new frontiers, today we continue to see that same brilliance in mathematicians like Dr Nira Chamberlain, a leading figure in British mathematics. 

Dr Chamberlain is an award-winning mathematician known for applying complex mathematical modelling to real-world problems, from predicting the lifetime costs of naval ships to solving industrial challenges across Europe and Africa. He holds a PhD in mathematical modelling and was named one of the UK’s top scientists by the Science Council. In 2020, he became President of the Institute of Mathematics and its Applications. Beyond his technical achievements, Dr Chamberlain is a passionate advocate for diversity in STEM, regularly speaking to young people about the power of mathematics and the importance of representation. 

Read more about Nira’s work here: Professor Nira Chamberlain OBE CMATH FIMA CSc – Professional Mathematician

A legacy of Black excellence in mathematics  

While Katherine Johnson and Dr Nira Chamberlain offer powerful examples of Black excellence in mathematics from the past and present, they are part of a much wider legacy. From Benjamin Banneker, who predicted solar eclipses in the 18th century, to David Blackwell, a pioneer in statistics and game theory whose work led to the Rao-Blackwell theorem, Black mathematicians have made profound contributions across centuries and continents. 

In the UK, figures like Francis Williams, a pioneering mathematics scholar in the 18th century who taught mathematics, and Dr Maggie Aderin-Pocock, a space scientist and science communicator who uses mathematical modelling in her work today and inspires young people through outreach and media, show how mathematical thinking continues to shape our understanding of the world. 

This Black History Month, I invite you to explore these stories further. Whether you are an educator, student, or simply curious, take time to discover the lives and legacies of Black mathematicians whose work deserves to be known, celebrated, and taught. 

An excellent place to start at would be The Open University Black STEM hub: created by and for Black STEM students  as a dedicated space by and for  Black STEM students. You can find out more about the students and staff involved here: Black STEM Hub | Faculty of Science, Technology, Engineering & Mathematics

OU Black STEM hub

Resources and further reading  

• BHM Open Learn resources: Black History Month | OpenLearn – Open University
• Open University library resources: Black History | Library Services | Open University
• The OU Race and ethnicity hub resources: Race and Ethnicity Hub | OpenLearn – Open University

Race and Ethnicity Hub

The Level 3 mathematics education modules at the Open University develop certain ideas (module ideas and frameworks) that can help us notice, structure and reflect on mathematical thinking. I’ll be using some of these to analyse my work on a puzzle from the Maths and Stats (M&S) student newsletter, Open Interval.

The joy in mathematics is in the doing, so do have a go yourself first!

FIGURE 1: The puzzle

I am particularly interested in the use of diagrams, so rather than jump into using numbers or x’s and y’s, I started with a ‘bar model’.

FIGURE 2: Coconuts as bars. Bounty?

While the bars were intended to be conceptual, the last two stages suggested a numerical solution: that they found 4 coconuts in the morning. I worked backwards from the 4 but it led to there being 11.5 coconuts at stage 2 ☹

FIGURE 3: Problem with fractions!

I’ll take a pause from sharing my mathematical work, and introduce one of our frameworks, Do – Talk – Record, covered in ME620 Mathematical Thinking in Schools.

FIGURE 4: DO TALK RECORD summary

While Do – Talk – Record (DTR) is presented sequentially, things aren’t that clear cut! The very act of doing with pencil and paper involves writing (recording) and the talking can be silent talking to myself or thinking aloud. Indeed, some of the writing in my work is my internal talk being made explicit. As doing, talking and recording are inextricably intertwined, the framework is meant to focus on the emphasis or intent at a particular stage, rather than divide activity up into separate boxes of Do, Talk, or Record.

FIGURE 5: Some later stages of recording

Indeed, having worked with it before, the DTR framework now prompts me to take stock when working on a problem, making explicit any emerging ideas.

There is another module idea that has an overlapping cyclical approach, Manipulate – Get a sense of – Articulate (MGA) covered in ME620 and in ME322 Learning and Doing Algebra. I manipulate my various representations of the number of coconuts at each stage, to get a sense of the mathematical relationships involved, which then helps me articulate better representations, which now become available for a further round of MGA.

The 11.5 coconuts (Figure 3) made me realise the puzzle may not be as easy I had initially thought. As fractional coconuts didn’t seem in the spirit of the puzzle, I would need to ensure that the numbers at each stage were positive integers. Such problems have a particular name, Diophantine problems, and can be notoriously difficult. So I decided some algebraic stock-taking may be helpful to ground further numerical work (trial and improvement?).

An early formal observation was that at each stage there would be 3k+1 coconuts for some positive integer k. Furthermore, other than the first stage, each subsequent stage would also need to have an even number of coconuts, 2k, the leftover once one share and one coconut (k+1) had been taken from the 3k+1.

Working backwards from a ‘final’ possibility such as 4 or 10 seemed less daunting than proceeding with solving recursive equations of the form N_2 = 2/3 (N_1 – 1) 🤪

FIGURE 6: Working backwards from 4, 7, 10, …

I had my first solution! I was convinced 79 was the smallest possible solution, so I was done. But that seemed quite unsatisfying. What more could I say or do? This leads me to Noticing Structure (in ME322), the final module idea I would like to share here. Join one of our modules to explore others! 😊

Ignoring the monkey’s singleton share, I need numbers that are continually divisible by 3; why have I not noticed that powers of 3 could be helpful?!

FIGURE 7: What happens with powers of three?

Looking more closely at the one successful sequence I had, and the unsuccessful ones(!), when working backwards, they all ended with a number that was 2 less than a power of three!!! Indeed, if I added in the ‘missing’ 2s, my sequences would start with a power of 3 and then go down to two-thirds at each stage.

FIGURE 8: Pattern spotting or noticing structure?

This structure, of powers of three, and that two-thirds would always then be an even number, aligned with the properties I had observed earlier (Figure 5). The offset of 2 wasn’t quite clear to me, though I knew some offset from  was needed to ensure the monkey’s share. This reminded me of the ‘Sharing 17 camels’ problem, and one idea could be to add two poison fruit to the pile of coconuts (which help with the division but remain unclaimed throughout). I had now (noticed) enough structure to use numerical, symbolic and even diagrammatic representations that would yield general solutions.

FIGURE 9: Testing numerical and diagrammatic conjectures

How can we be sure that these patterns will always work? I will leave that with you to explore!

As a final takeaway message, the ME322 materials say, “Choosing particular representations can help with noticing structure”. Something for me to bear in mind when trying to crack future puzzles!

This post is written by Gerry Golding, an OU staff tutor in Northern Ireland, who led the mathematics education team in creating a free flexible resource for improving adult numeracy and confidence with maths.

For many adults, young and old in NI, mathematics can be perceived as a barrier to career entry and/or progression. Everyday mathematics is often a hidden source of anxiety, left un-addressed for fear of ridicule. Even competent people avoid being put on spot when it comes to say splitting the bill after a dinner with friends in a restaurant.

Restaurant bill from the Coming Back to Maths video: who are you?

Working in a maths support centre at the University of Limerick before I moved to the OU, a common theme I experienced when talking to students about their first visit was the number of times they had gotten as far as the door, but couldn’t walk through it because of anxiety or some past unresolved issue with maths. For some, it took the support of a friend coming with them to walk them through the door of the centre.

The goal of the” Everyday Maths NI Multiply Project” is to be an enabler, to give people like this the confidence to walk through the “maths learning” door, to start, or restart, their maths journey and quietly build some resilience at their own pace.

Where did it start?

One of the flagship initiatives of the UK Shared Prosperity Fund (UKSPF) launched on the 13 April 2022 was the Multiply project. Funding was made available to support local authorities and devolved administrations in delivering tailored programmes to help adults improve their functional maths skills through free, flexible learning options such as personal tutoring, digital training, and community-based courses. Each region received a portion of the funding based on its UKSPF investment plan.

Gerry (left) launching Everyday Mathematics at Belfast City Hall

In Northern Ireland, the Multiply project aimed to improve adult numeracy skills by offering free courses tailored to fit around people’s lives and delivered through further education colleges, universities, local councils, and community organisations. Funded from 2024-5, the programme targeted over 3,000 adults across the region, addressing a significant skills gap as highlighted by the 2022 Employer Skills Survey, which found that a lack of basic numeracy contributed to a quarter of the skills-shortage vacancies in Northern Ireland.

Multiply in Northern Ireland included innovative pilots, such as numeracy training for non-native English speakers, with early results showing high success rates.  The OU in NI collaborated with our Mathematics Education group in the OU School of Mathematics & Statistics  to design a successful bid under the “Engaging Mature Learners – Making it Count” theme, creating materials that are available whenever they are wanted, for as long as they are needed.

The OU contribution

Updating existing content and education technology specialists, we created interactive “Everyday Maths Northern Ireland”  courses and learning materials on OpenLearn, the Open University’s free learning platform. The content in the two 48-hour badged courses maps the Essential Skills Numeracy curriculum in Northern Ireland. Each course is developed across four themes

1. Working with Numbers
2. Units of measure
3. Shape and Space
4. Handling data
   

   The home page of Everyday maths 1

The design is simple – Everyday Maths 1 is linked to Level 1 Essential Skills and Everyday maths 2 is linked to Level 2 Essential skills. And it is popular – Everyday Maths 1 has had 98,000 visits in the ten months since it started in October 2024.  We have tried to match our methods to follow how adults were taught mathematics in school and show how children are taught now.  This means parents can help their children with homework and feel confident that both methods work.

The courses are supported by additional learning materials.

We designed four bite-sized interactive everyday maths activities that teach a topic and check your understanding in less than 15 minutes.

• Understanding Risk,
• Statistics in the News
• Ratios and proportions.
• Keeping things in proportion – using our visual skills to navigate a data and image-rich world

For a taster, we drew on our mathematics education research and the experiences of OU students to create three short inspirational videos:

How it looks on Open Learn

• Coming back to Maths: recognising anxiety and building resilience

• From zero to hero: it’s never too late, a student’s story

• Doing Maths with AI apps: why learn maths when AI can do everything? The myth that maths is just about calculations.

In the next post we will tell you who we designed these materials for and what is happening next.

What is engaged research?

Public engagement with Higher Education research (often shortened to HE-PE) is all about the different ways universities engage the wider public with their research and activities. The goal isn’t just to inform people, but to build positive, two-way relationships between universities and communities. According to the UK National Co-ordinating Centre for Public Engagement, it should involve genuine interaction and listening, with the aim of generating mutual benefit (NCCPE, 2020). Many UK academics feel a strong moral obligation to get involved in public engagement, and participation is often based on intrinsic rewards, such as wanting to share their research with broader audiences (Watermeyer, 2016), but academics also need to see how it benefits their own personal and professional development. Whilst most academic researchers agree that HE-PE should be based on a two-way relationship in practice it often follows a ‘deficit model’ approach, where academics decide what to share, when, and how, and the public is expected to just take it in (Grand et al., 2015).

School students engaging with tiling puzzles at the Open University Aperiodic Tiling exhibition

Over the last decide, universities have been encouraged to rethink how they engage with the public, to not just present research to audiences, but to work with and include publics in the creative process (Grand et al., 2015). This is where engaged research comes in, a concept coined by Open University researchers (Holliman et al., 2015). Rather than one-off events or top-down communication, it’s a more intentional and collaborative approach. Instead of academics doing the research in isolation and then sharing it afterwards, engaged research brings in community members, stakeholders, or even school students as collaborators at different stages of the research, including sometimes at the very start of the research process (Holliman et al., 2015). It’s about breaking down the barrier between expert and audience and creating a more equal, inclusive way of doing and sharing research. Researchers and the public work together to ask questions, gather data, and make sense of the results. Everyone brings different experiences and knowledge to the table and different forms of knowledge, not just academic knowledge, are treated as valuable. Engaged research is built on relationships, trust, and shared learning.

The challenge is that it is not easy to achieve engaged research. According to Holliman et al. (2017), engaged research can take more time, more effort, and is often far more labour intensive than traditional academic research. It requires planning, communication, and can require a willingness to let go of control. Barriers such as research funding, short timeframes or university policies can make it difficult to plan for engaged research. For these reasons, some researchers still prefer to continue with more established models, because they feel simpler or more familiar. This means the most common kinds of HE-PE are still one-way, ‘top-down’, events including researcher led lectures, masterclasses, and demonstrations.

Why is it important to move beyond the deficit model of HE-PE?

Whether they are aware of it or not, academic researchers in mathematics and statistics hold power over the knowledge they create through their research. For example, they not only choose what to research (though this can be constrained by research funding) but they also make decisions about how to develop this research, whether to involve non-academic stakeholders in the planning process or data collection stages (Medvecky, 2018). They also choose how the research is shared within academic and non-academic communities, including which journals to publish with, which science fairs to present at, which schools or community groups (if any) to visit etc. This means that researchers have a responsibility to consider epistemic justice,  or fairness in knowing, that is, to consider how the knowledge they create is equitably distributed and beyond that, to make sure it is created fairly.

The concept of epistemic justice was developed by British philosopher Miranda Fricker (2017) to describe the ethics of knowledge production. It describes a fairness in the way knowledge is shared, created, and valued. In simple terms, it’s about making sure everyone has a fair chance to know things, and to be recognised as someone worth listening to.

Fricker (2017) describes two main types of epistemic injustice: Testimonial injustice and Hermeneutical injustice.

Testimonial injustice happens when someone’s knowledge or experience isn’t taken seriously because of who they are, or in contrast when someone’s knowledge is overly trusted because of who they are. For example, a professor in mathematics may be considered an expert over a hobbyist mathematician, even if the topic in questions is outside of the professor’s expertise and the hobbyist has a great deal of knowledge in this area. If the hobbyist’s opinion is dismissed because they are seen as a non-expert, that’s a form of testimonial injustice.

In 2022, a retired print technician and amateur mathematician, David Smith, showed the value of non-expert knowledge by making a significant discovery in the field of aperiodic geometry through creating an aperiodic monotile: a single aperiodic tile which could tile the plane. This discovery helped solve the previously unsolved Einstein problem.

Hat tiling created by David Smith

Hermeneutical injustice is when people don’t have the tools, language, or opportunity to fully understand or express their experiences. In a mathematics and statistics research context, this might mean not being supported to ask questions, challenge assumptions, or explore new ideas. For example, when a new mathematical discovery is made, if it is shared only in academic journals, using very technical language, public audiences may not have the tools to understand or question the discovery.

When universities rely on traditional models of public engagement, groups like school students, community members, or hobbyists can be unintentionally excluded from sharing their knowledge or from being able to learn, question and critique new knowledge. Not because they don’t have anything to offer, but because they aren’t always seen as serious contributors or given the opportunity to contribute. That’s not just a missed opportunity to learn from different groups of people and to expand knowledge production and exchange, it is also a form of epistemic injustice.

Holliman (2019) suggests that engaged research can help tackle issues of epistemic injustice by opening up space for more people to be seen, and to see themselves, as knowers. It values different ways of understanding the world, not just what’s published in academic journals. And that makes research fairer, more inclusive, and often more relevant to real-life challenges.

A-level students working on mathematical research at the Open University

Further reading

Rick Holliman, Professor of engaged research, gave his inaugural lecture entitled ‘Fairness in knowing’, about engaged research and epistemic justice. You can watch and read it here: Fairness in knowing’: How should we engage with the sciences? | The Open University

References

Fricker, M. (2017). Evolving concepts of epistemic injustice. In The Routledge handbook of epistemic injustice (pp. 53-60). Routledge.

Grand, A., Davies, G., Holliman, R. and Adams, A. (2015) ‘Mapping Public Engagement with Research in a UK University’, PLoS ONE, 10(4) pp. 1–19.

Holliman, R., Adams, A., Blackman, T., Collins, T., Davies, G., Dibb, S., Grand, A., Holti, R., McKerlie, F., Mahony, N., and Wissenburg, A. eds. (2015). An Open Research University. Milton Keynes: The Open University.

Holliman, R. (2019). Fairness in knowing: How should we engage with the sciences? The Open University, Milton Keynes. Online: http://oro.open.ac.uk/60416

Medvecky, F. (2018). Fairness in knowing: Science communication and epistemic justice. Science and engineering ethics, 24(5), 1393-1408.

National Co-ordinating Centre for Public Engagement (2020) What is Public Engagement? Available at: https://www.publicengagement.ac.uk/about-engagement/what-public-engagement.

Watermeyer, R. (2016) ‘Public Intellectuals Vs. New Public Management: The Defeat of Public Engagement in Higher Education’, Studies in Higher Education, 41(12), pp. 2271–2285. Doi: 10.1080/03075079.2015.1034261.

This post is written, in both English and Welsh, by Dr Delyth Tomos, an OU Associate Lecturer who tutors on modules in mathematics and statistics, and engineering.

Delyth has recently co-led a project looking at Welsh-medium tuition in mathematics.  To learn more about the project, click here  

Ysgrifennwyd y neges hon, yn y Gymraeg ac yn Saesneg, gan Dr Delyth Tomos, Darlithydd Cyswllt gyda’r Brifysgol Agored, sy’n diwtor ar fodiwlau mewn mathemateg ac ystadegau, a pheirianneg.

Yn ddiweddar mae Delyth wedi cyd-arwain prosiect yn edrych ar addysgu mathemateg drwy gyfrwng y Gymraeg.  Er mwyn gweld mwy o wybodaeth am y prosiect, cliciwch yma.

As someone who has lived and worked in North Wales since birth, being exposed to two languages, Cymraeg/Welsh and English, is pretty much a way of life. Children are taught in both languages from an early age, and develop linguistic skills that allow them to participate fully in education, work, family and social activities in two languages, thus maximising the opportunities available to them.  Discussions in formal and informal settings are frequently conducted through both languages, switching from one to the other, and most of us do this with ease, hardly realising that what we are doing is much more complicated linguistically than we possibly realise.

Welsh landscape. Image credit David Kjaer / Nature Picture Library / Universal Images Group.

A bilingual education involves subjects being taught in both languages, and effective strategies have evolved over the decades, underpinned by a wealth of research in countries where living through the medium of more than one language is the norm (Spitzer, 2016 and Mukan et al, 2017). These strategies promote constructive learning where the use of two languages enhances a learner’s resilience and effectiveness within specific subjects as well as their language skills in general.

Learning mathematics through the medium of both Cymraeg and English encourages learners to acquire and develop flexible approaches to their studies. Understanding and learning how to solve mathematical problems requires a learner to develop a subject-specific vocabulary which needs to be incorporated within the learner’s wider language skills. In mathematics, a learner needs to be able to  describe  and interpret a problem, analyse and select relevant pieces of information from a given situation, organise the information, consider how this information may be used to address a particular problem, select and justify suitable mathematical methods, undertake various mathematical calculations and manipulations, and finally, to interpret their solutions or results in order to address the original problem.   It is clear that these strategies are complex, and it can also be seen that most of these skills are deeply embedded in language.

School sign in English and Welsh languages. Image credit David Hunter / Robert Harding World Imagery / Universal Images Group

When discussing mathematical concepts and terms in different languages, learners have opportunities to make connections with previous knowledge in both languages, and this, in turn helps them to construct their learning of mathematical ideas in both languages. Mathematical problems may be described and framed in a similar manner in two different languages, but the translation will not be exactly the same. Translation is not a matter of substituting one word from one language to an equal term in another language. Effective translation requires an equivalent adaptation of meaning in both languages in addition to syntactic flexibility and choosing suitable terms to delineate a problem in a manner that is accurate and helpful. Being creative and flexible as part of the translation process results in mathematical problems being conceptualized from two slightly different  directions, resulting in a deeper understanding of how to address problems.

Learning mathematics (and other subjects) through the medium of two languages thus provides learners with opportunities to fully engage in learning, in both their first and second language, and to engage with concepts from two slightly different directions. This in turn encourages them to become flexible, creative and resilient learners  and this naturally benefits mathematics learners.

Manteision astudio mathemateg mewn dwy iaith (Cymraeg a Saesneg)

Fel rhywun sydd wedi byw a gweithio yng Ngogledd Cymru ers ei geni, mae dod i gysylltiad â dwy iaith, Cymraeg a Saesneg, yn ffordd o fyw. Caiff plant eu haddysgu yn y ddwy iaith o oedran cynnar, a byddant un datblygu sgiliau ieithyddol sy’n caniatáu iddynt gymryd rhan lawn mewn addysg, gwaith, gweithgareddau teuluol a chymdeithasol mewn dwy iaith, gan wneud y mwyaf o’r cyfleoedd sydd ar gael iddynt.  Caiff trafodaethau mewn sefyllfaoedd ffurfiol ac anffurfiol eu cynnal yn aml drwy’r ddwy iaith, gan newid o’r naill i’r llall, ac mae’r rhan fwyaf ohonom yn gwneud hyn yn rhwydd, prin yn sylweddoli bod yr hyn yr ydym yn ei wneud yn llawer mwy cymhleth yn ieithyddol nag yr ydym o bosibl yn sylweddoli.

tirwedd Cymru. Credyd delwedd David Kjaer / Llyfrgell Lluniau Natur / Grŵp Delweddau Cyffredinol.

Mae addysg ddwyieithog yn golygu bod pynciau’n cael eu haddysgu yn y ddwy iaith, ac mae strategaethau effeithiol wedi datblygu dros y degawdau, wedi’u hategu gan gyfoeth o ymchwil mewn gwledydd lle mae byw trwy gyfrwng mwy nag un iaith yn norm. (Spitzer, 2016 A Mukan et al, 2017). Mae’r strategaethau hyn yn hybu dysgu adeiladol lle mae’r defnydd o ddwy iaith yn gwella gwydnwch ac effeithiolrwydd dysgwr o fewn pynciau penodol yn ogystal â’u sgiliau iaith.

Mae dysgu mathemateg trwy gyfrwng y Gymraeg a’r Saesneg yn annog dysgwyr i gaffael a datblygu ymagweddau hyblyg at eu hastudiaethau. Mae deall a dysgu sut i ddatrys problemau mathemategol angen i ddysgwr ddatblygu geirfa pwnc-benodol y mae angen ei hymgorffori o fewn sgiliau iaith ehangach y dysgwr. Mae angen i’r dysgwr allu disgrifio a dehongli problem, dadansoddi a dewis darnau perthnasol o wybodaeth o sefyllfa benodol, trefnu’r wybodaeth, ystyried sut y gellir defnyddio’r wybodaeth hon i fynd i’r afael â phroblem benodol, dewis a chyfiawnhau dulliau mathemategol addas, gwneud cyfrifiadau a thriniadau mathemategol amrywiol, ac yn olaf, dehongli eu hatebion neu ganlyniadau er mwyn mynd i’r afael â’r broblem wreiddiol.  Mae’n amlwg bod y strategaethau hyn yn gymhleth, a gellir gweld hefyd bod y rhan fwyaf o’r sgiliau hyn wedi’u gwreiddio’n ddwfn mewn iaith.

Arwyddion ysgol yn y Gymraeg a’r Saesneg. Credyd delwedd David Hunter / Robert Harding World Imagery / Grŵp Delweddau Cyffredinol.

Wrth drafod cysyniadau a thermau mathemategol mewn gwahanol ieithoedd, caiff dysgwyr gyfleoedd i wneud cysylltiadau â gwybodaeth flaenorol yn y ddwy iaith, ac mae hyn, yn ei dro, yn eu helpu i adeiladu eu dysgu o syniadau mathemategol yn y ddwy iaith. Gellir disgrifio problemau mathemategol a’u fframio mewn modd tebyg mewn dwy iaith wahanol, ond ni fydd y cyfieithiad yn union yr un fath. Nid yw cyfieithu yn fater o amnewid un gair o un iaith i derm cyfartal mewn iaith arall. Mae cyfieithu effeithiol yn gofyn am addasiad cyfatebol o ystyr yn y ddwy iaith yn ogystal â hyblygrwydd cystrawennol a dewis termau addas i amlinellu problem mewn modd sy’n gywir ac yn ddefnyddiol. Mae bod yn greadigol a hyblyg fel rhan o’r broses gyfieithu yn arwain at gysyniadoli problemau mathemategol o ddau gyfeiriad ychydig yn wahanol, gan arwain at ddealltwriaeth ddyfnach o sut i fynd i’r afael â phroblemau.

Mae dysgu mathemateg (a phynciau eraill) trwy gyfrwng dwy iaith felly yn rhoi cyfleoedd i ddysgwyr ymgysylltu’n llawn â dysgu, yn eu hiaith gyntaf a’u hail iaith, ac i ymgysylltu â chysyniadau o ddau gyfeiriad ychydig yn wahanol. Mae hyn yn ei dro yn eu hannog i ddod yn ddysgwyr hyblyg, creadigol a gwydn, ac mae manteision amlwg i hyn ar gyfer dysgwyr mathemateg.

References/Cyfeiriadau

Mukan, N.  et al (2017). The Development of Bilingual Education in Canada. Advanced Education, Issue 4(8) pp. 35 – 40.

Mukan, N. et al (2017). Datblygiad Addysg Ddwyieithog yng Nghanada. Addysg Uwch, Rhifyn 4(8) tt. 35 – 40.

Spitzer, M (2016). Bilingual Benefits in Education and Health. Trends in Neuroscience and Education, Volume 5, Issue 2, pp 67-76.

Spitzer, M (2016). Buddion Dwyieithog mewn Addysg ac Iechyd. Tueddiadau mewn Niwrowyddoniaeth ac Addysg, Cyfrol 5, Rhifyn 2, tt 67-76.

This post is written by Ben Leslie, winner of the Stanley Collings prize in 2024.

The Stanley Collings prize is awarded annually by the School of Mathematics and Statistics. The prize is awarded to the student who best combines innovation in devising materials suitable for learners and insightful analysis of their learning. The post is a rewritten version of his final assignment in Learning and Doing Algebra (ME322).

Congratulations Ben!

While studying the module Learning and Doing Algebra, I worked with an adult learner, who I call Ina, and who is completely blind.  Mathematics is generally taught as a visual subject so my objective was to make the tasks accessible but also to introduce concepts such as graphical illustrations that are common in the workplace.  I chose the following task from the module to introduce graphs and explain how to use them.

Task 11 What’s the story?

The following graphs provide information on two cars (car A and car B):

Comparing cars A and B

(a) Are the following statements true or false?

(i) car A is more expensive than car B.

(ii) car B is faster than car A.

(iii) car A costs less to insure than car B.

(iv) the older car costs more in road tax.

(v) the faster car costs more to insure.

(b) Write a short description for car A and car B.

(c) Use these axes to mark crosses to represent car A and car B.

Axes for comparing cars A and B

I printed Braille graphs and selected dots or distinctly shaped beads to represent the cars. I wanted Ina to develop the algebraic reasoning to understand how the distance from the origin on each axis represented the value of the axis title.

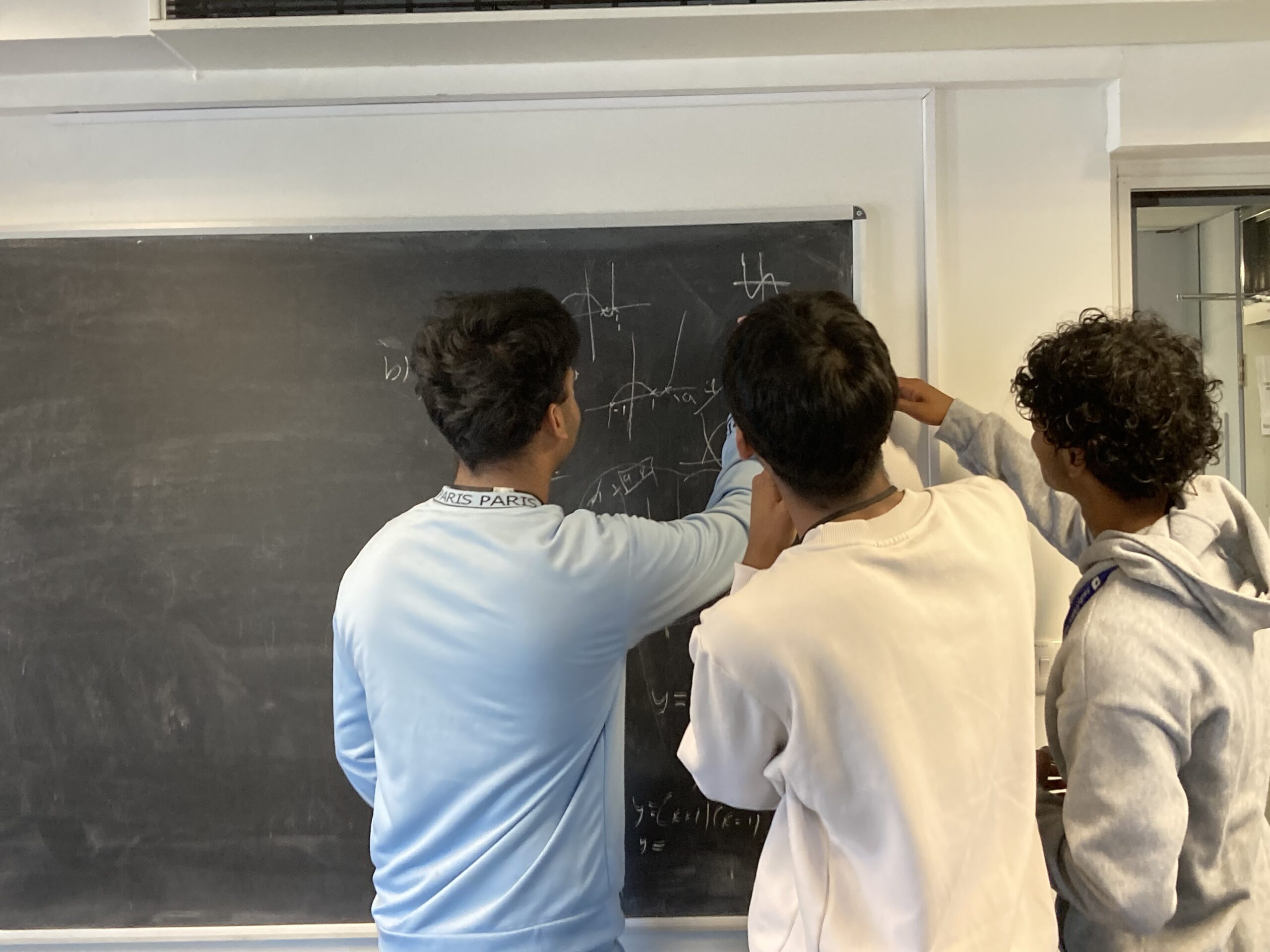
I printed a line of Braille dots for each axis and read aloud each task instruction and question. I mentioned that she need not give exact values, only its relation to the other car, for example, ‘Car A is older than B.’ She used this language when reasoning her responses to the statements. For statement (a)(i), she answered ‘False, car B is more expensive because it is younger.’ I re-phrased the question to, ‘Ignoring age, which car is more expensive?’ (I will elaborate why later, but I wanted her to practise using the y-axis.)  She finished the remaining statements without much difficulty and gave good descriptions of the cars that I recorded.

Ina’s answers

In part (c) Ina’s difficulty using the y-axis resurfaced when she tried to represent both variables on the x-axis. For example, she correctly placed car A on the x-axis for value before moving it along the same axis to identify the cost of insurance.

Using the horizontal axis for both variables

With a simple prompt she recognised and corrected it.

The last part of the question was to imagine a third car, C, describe it and add Car C to all the graphs. Ina described car C using extreme terms: “super- valuable, super old – its a vintage; very slow, massive engine, free road tax, expensive insurance”.

I influenced her choice to give car C free road tax. It would be eligible for free road tax as it was vintage, but also, it would give her a zero value to work with which I wanted to see her represent in the graph, especially because road tax was the y-axis which she found difficult. She managed this successfully.

When analysing my learner’s work, I identified three module ideas which are related to her key moments and decisions. They are relations, covariation and Invariance and change (all Open University, 2023).

Relations

I described letting my learner know that she did not have to assign values to each variable. Although there was nothing wrong with doing this, I felt it was important for her to be able to compare the cars without necessarily doing arithmetic. Inequalities can be used in algebraic expressions and being more confident with using the terminology ‘greater than’ and ‘less than’ will enable her to progress future mathematical study.  This was also an important skill to have for the true or false statements, which were expressed as inequalities.

Covariation

When my learner said car B was more expensive because it was younger.’ I re-phrased the question to, ‘Ignoring age, which car is more expensive?’ Although an onlooker may have recognised that she had given the correct answer and possibly even jumped ahead to identifying covariance, I wanted to double check that she had used the y-axis and was not just making the general assumption that new cars are more expensive than used cars. I was glad I checked, as it turned out that she had not used the y-axis. This also revealed that she had more difficulty reading the y-axis than the x-axis which is something we then worked on throughout the task.  After ensuring she was reading the graphs correctly, I revisited her first answer and explored covariance. I congratulated her for pointing out there is often a relationship between the age and value of items and explained that covariance does not imply causation. I encouraged her then, throughout the rest of the tasks, to identify if the covariations between different aspects of the cars make sense, for example, if the engine is larger,  would the max speed be expected to change? It was interesting to watch which covariances she carried through in car C. For example, she continued with age and speed varying together, but age and value varying separately as she accounted for it being vintage.

Invariance and Change

This task was set out well and allowed for my learner to not only explore different covariations, but also to change which relationships are explored. In part (c) two empty graphs were given. The change here was that the cost to insure, which was on the x-axis in the previous graph, became the y-axis in the new graph. Additionally, the value of the cars, which was previously a y-axis became an x-axis. This helped my learner ground her understanding of the y-axis as she converted the approximate distance of y-variable from the origin, into an x-variable and vice versa with the cost to insure variable.

Reflection

When choosing and preparing the tasks throughout this module, I had focused on improving my abilities to make them accessible and meaningful to my blind learner. On reflection, my preparations have improved dramatically from her first tasks, where I used random objects at hand as representations of numbers or symbols, to now where in this example I have carefully thought out how to write the task in an accessible format with clear meaning. This allowed me to follow Bruner’s modes of representation (Open University, 2023) to help use tangibility to lay the foundation for concepts which can later be simplified into Braille symbols or even calculated mentally.

I often had to apply the module concept of using variation in teaching to ensure that my learner grasped the concepts intended in the session (Open University, 2023). This would range from me needed to rephrase questions, like I did in this task, or writing new problems that would stretch my learner’s thinking. This is related to the module idea of freedom and constraint (Open University, 2023), and I would often try to introduce or remove a constraint in her tasks to  enhance the learning experience, in this task I did that more subtly by encouraging her to use free road tax for car C.

Another module concept that I focused on was conjecturing and convincing (Open University, 2023). I liked the idea of allowing my learner to create her own conjectures based on the evidence in front of her, and then by testing that, was able to convince herself she was right. I really felt this was something important I wanted my learner to experience as I didn’t want her to have my educational experience – knowing what the right answer was, without knowing  it was the right answer or  it came from.

Overall, I have been struck by how the module ideas, when combined, demonstrate a very explorative and exciting way to teach and learn algebra. Before starting the module, I was anticipating there would be one or two clear-cut, tried and tested methods of drilling algebraic concepts into student’s heads. But I have enjoyed how the learning experience has been more focused on enabling the learner to learn and discover for themselves and share that excitement with their teacher, who can also learn or observe something new in every lesson.

References

The Open University (2023) ME322: Learning and doing algebra.