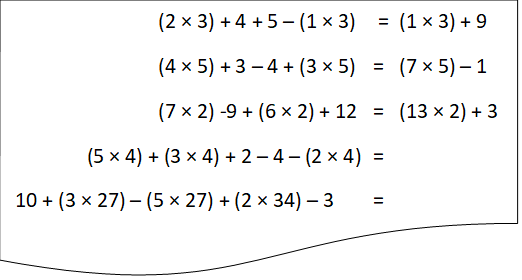This post is written by Esther Wheatley, winner of the Stanley Collings prize in 2021.
The Stanley Collings prize is awarded annually by the School of Mathematics and Statistics. The prize is awarded to the student whose Mathematics Education assignment best combines innovation in devising materials suitable for learners and insightful analysis of their learning.
Congratulations Esther!
I always enjoyed maths and found it easy to focus on, even when Chronic Fatigue Syndrome reduced my school attendance. Having become a Teaching Assistant, I decided to study Maths further with a view to teaching. The Open University is great provider which allowed me to study around my circumstances and commitments: I highly recommend it. However, while I loved the maths modules, my decision to change to “Mathematics and its Learning” dropped me into reflective essay writing. Like others, I struggled with new ways of thinking, so I deferred a module while trying to figure it out. The deferment enabled development through each module, and my grades improved dramatically. However, I was extremely surprised to find myself cowinner of the Stanley Collings prize for tasks devised in the final assignment of the module Developing Thinking In Algebra. Here, I share modified reflections on the tasks I did with my adult learner, who I will call Amy. I have focused on one task, but allowed some comparison with the second to remain. The task I have chosen uses Algebra tiles, which are a great resource that I am pleased to introduce to a wider audience.
Amy and I worked together for my final two modules. Most lessons were on Zoom, which worked well because I could record and transcribe sessions, giving an accurate record to reflect on. Amy emailed me her memories after a couple of weeks. For health reasons, Amy missed a lot of school and so displays mathematical anxiety and low expectations. However, the Developing Thinking in Mathematics modules premise that every learner has the ability to specialise and generalise, imagine, express, organise, classify, conjecture and verify (referred to as mathematical powers.) I saw it as my role to encourage Amy in the awareness and use of these powers to learn and build her confidence.
The Plan
I naturally lean to giving direct instruction but, in adapting and transferring my understanding to teach others, a gap can be created between what they learn and the underlying concepts – this is known as didactic transposition. Therefore, attempts to impart my excitement and understanding often lead to behavioural, rather than conceptual, instruction or overwhelm my learners. To avoid this, I aimed for tasks that let Amy work independently and use her mathematical powers to discover generalities for herself, which is considered key to developing algebraic thinking.
Algebra tiles
I devised the task around algebra tiles. Algebra tiles are manipulatives that attempt a concrete representation of variables and units.
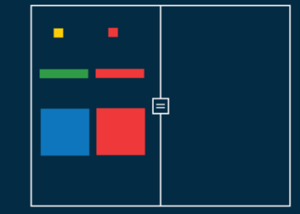
Small squares represent units
Narrow rectangles represent a variable (e.g. x)
Large squares represent the variable squared (x2)
Each has a red side and a coloured side, with the red representing negative value. Hence the overall value in the image here is 0 as each red tile cancels out its counterpart.
My physical tiles have two variable lengths in different colours and therefore two sizes of larger square and also a rectangle representing the multiplication of the two variables (e.g., xy)
I used an electronic version to replace physical algebra tiles with manipulable images because they were more easily accessible with Zoom and less limited in number. The app can be accessed at https://didax.com/apps/algebra-tiles/
Enactive, Iconic, Symbolic and Manipulate – Get a sense of – Articulate
I first discovered algebra tiles when looking for manipulatives for intervention groups, having found that physical objects, pictures and practical examples made it easier for my students to understand and connect to topics. Like those learners, Amy shows apprehension with algebraic symbols and numbers, but is confident with pictures and physical objects, so I felt algebra tiles could provide an accessible link through familiar concrete materials to the symbolic representation that she found daunting.
The value of multiple representations and progression from concrete through iconic to symbolic representations is well documented. For instance, a concrete, pictorial, abstract approach, influenced by Piaget, is central in mastery curricula (Drury, 2018). Bruner (1986) also proposed three modes of representation which follow each other in cognitive development: Enactive (involving physical interaction and activity with concrete objects), Iconic (representation through pictures) and Symbolic (the use of language and symbols). The modes may relate to phases of development in terms of age, but also stages for any new learning. They underpin the manipulate-get a sense of- articulate (MGA) construct, where learners manipulate familiar objects or understanding, getting a sense of a new ideas that become clearer until a newly understood concept can be articulated. The process is cyclical, or spiral-like, as the new understanding can be further manipulated and built on to gain additional insights.
The Task
The aim of the activities was to simplify expressions by grouping like terms, but the tasks are also an example of diverting attention to automate, since they provided experience working with variables and alternative representations, which Amy needed practice in.
I first created examples with the algebra tiles, which are familiar-looking objects which could be virtually manipulated…

… The second section used numbers which are familiar to Amy, but she is less confident with numbers than objects.
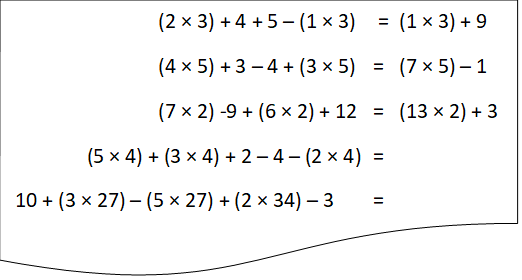
Finally, I introduced algebraic symbols, which Amy is least confident with. These I gave first in zoom chat and then verbally.
I chose to make the initial questions in the first two sections completed examples, rather than questions to be answered (see above.) I then promoted the strategies of “say what you see” and “same and different” to encourage Amy to get a feel of and make sense, for herself, what was going on. I was concerned that Amy would make equivalences between the manipulatives and be confused by spacing, but I determined to let her create and revise her own conclusions rather than providing immediate guidance on this.
Learner Activity
Saying what she saw, Amy immediately recognised the equals sign as expressing a relationship, but sought confirmation.
“Well, you’ve got the… the top picture is like 2 different pictures linked together with the equals sign so they must be relationship between the left hand side and the right hand side umm… So are the ones on the left hand side supposed to be equal to the ones on the right hand side? Is there a mathematical equation between them?”
Other observations included size, shape, colour and position as well as possible connections, such as that a rectangle was worth four small squares.
“ … you’ve got three equal length rectangles 2 green 1 red and then you’ve got two little units like single units joined together uh, of red and yellow umm, which seem to be half the length of one of the rectangles so in a sense you’ve got three and a half of the rectangles there and then the other side you’ve got one rectangle.”
“I think in my mind I had thought it was the same value all the time but I couldn’t work out if I could put four single units together to equal the same amount as the rectangle”
Amy showed anxiety that she had to express the relationship and could not really see it but immediately conjectured that the red tiles were “minuses” apparently taking them to represent action on adjacent tiles, rather than value. Carefully giving my solution to an extra question enabled Amy to modify her conjecture, along with her understanding of the role of space and equivalence.
“I don’t think I could write it down. I can’t… I can’t see the relationship. I can see that y’know, there are like what you might call tens and units but I can’t see how unless you say umm, unless the reds are minuses if you like… ”
“the reds have eliminated the ones next to them and left the others”
After the new example:
“ok so I’m thinking that the red square deletes the blue square and the red rectangle deletes the green rectangle”
“the only other possible way you could do it I can see is if you could take a little square out of the big square, which I don’t know if you can do”
“those of the same value they eliminate”
That she had discovered this herself was the highlight of the lesson for Amy, along with making up her own examples, occurring after explaining the significance of the tiles.
“I felt jolly pleased with myself that I worked out it was minus”
Via email: reds were minuses which took out a rectangle or square of equal value… I was pleased to pick this up fairly quickly and be able to start to make up my own equations.
Showing her understanding of the general nature of the tiles, Amy gave examples of integers they could represent, extending her understanding when surprised by my example of a decimal.
“yeah so they’re all just different values but the size of them makes them the same value as others of the same size”
“well it could be anything really, 200, 100, 60, 80”
Me: 32.752
Amy: “pardon?! laughs, 5.5. But the little ones are always going to be one” (specialising from the general)
Moving to numerical questions, Amy’s attention was on the operations, and she performed the calculations, checking each side in given cases and either leaving a single answer or changing it to a similar form as the given cases on the rest.
“ok, so 2 x 6 is 6, plus 4 is 10, plus 5 is 15, minus 1 times 3, so one three is 3, so minus three is 12 = three plus nine is twelve, so that’s okay.
So four times five is 20, plus 3 = 23, minus that is 19, plus 3 times 5 that’s 15, hang on I’m just going to write some down (carries on working out totals). So now we’ve got the ones I need to fill in. That’s 20 plus 12 is 32, plus 2 is 34, minus that is 30, minus 8 is 22. So how do I write that down.. 22 equals 5 times 4 plus 2”
A key moment was Amy’s encounter with a more difficult question and the prompt to use algebra tiles to solve it.
“well this is the sort of thing you do in your puzzle book, which I’m hopeless at”
Me: try using your algebra tiles, see if it helps.
“I don’t know whether I can do it with the algebra tiles. Umm ok um, this is 10 (green tile) this is 27 (blue square) not going to fit them all in. Umm so now how do I do minus five of those? can I work it out on paper?”
Me: yeah, do whatever you like but do think about how you can do minus five of those
“well I could take away… oh I see, ok, ok umm” (erases three and puts in two reds)
From here, after initial worry, Amy engaged with algebraic questions, quickly becoming independent of algebra tiles, so that I wondered if it would have been better to have skipped the numerical examples. However, Amy felt that the combination of all aspects had been important and that without both she would have been unable to complete the algebraic questions, suggesting that the mind-set change as Amy moved from calculation to working out how to express with algebra tiles was important in building her understanding of the role of variables and symbols.
Amy: oh mate, hang on. You see this is where my brain suddenly goes whoosh. You see the others I could work out eventually with all the numbers in
Me: so try with your tiles
Amy: ok, right we’ll call this a, so we’ve got 2 a’s oh, yeah, two times a, plus 5 (putting out 5 yellows) plus four times a (puts out another 4 green) this isn’t going to work I don’t think minus three, ok (gets the eraser)
Me: I’d like you to show the minus three
Amy: well I’m trying to get rid… oh, ok silly me.
Me: And then show me the other side
***
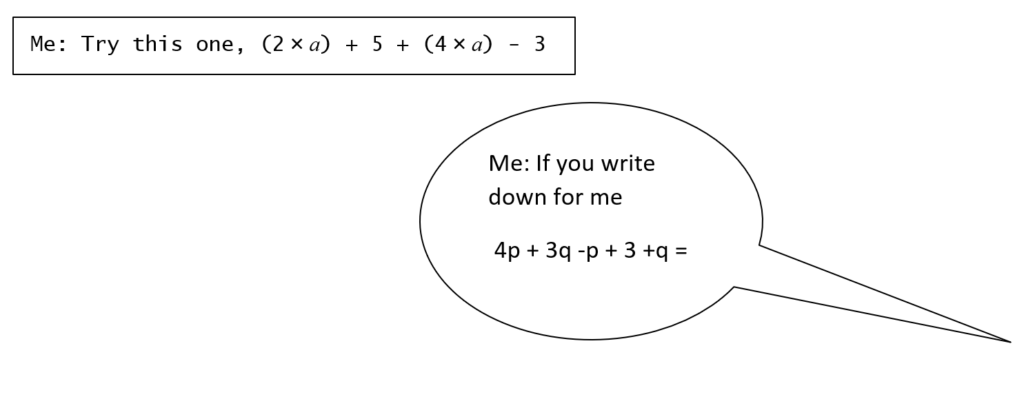
Me: so write down on paper for me, 3b + 19 -2 +5b
Amy: I would say that equalled 8b + 17
Me: yeah do you think you would have got that at the beginning?
Amy: no
Me: do you think you’d have got it before you did the things with the numbers in?
Amy: no, probably not
After two weeks, Amy emailed me with her memories, having had no further exposure to the topic. She wrote:
…Reds were minuses which took out a rectangle or square of equal value. …gradually I could see how the equations could be put into algebraic form. So 2 x 25 + 25 = 75 could be written as 2P + P = 3P. Replacing numbers with letters allows you to use the same equation with different values…
Reflections
The mathematical powers of imagining and expressing, organising and classifying, conjecturing and convincing, and specialising and generalising, were evident throughout the task and, as hoped, activity is best described by the MGA construct. Imagining placement, action and modification of tiles, manipulating in her head, helped Amy make and imagine conjectures, gaining a sense of what was happening (maybe the reds are minuses) and convincing herself by comparing given special cases (individual examples) to develop a sense of generality (the reds always take away adjacent tiles). Verbal expression revealed thinking, while placing algebra tiles expressed/articulated conclusions which were compared again, sometimes modified as Amy made new conjectures (reds take away corresponding tiles), getting a sense of whether they fitted perceived relationships. Continuing cyclically as new special cases were introduced, the same processes enabled development to symbolic examples, Amy first expressing with tiles, manipulating to get a sense of how to simplify and relating back to symbolic forms, eventually manipulating symbols only. Easily overlooked was Amy’s power to classify according to shape, size and colour, and to organise and recognise order, which enabled her to determine which terms were equal and equate tiles to symbols. The powers intertwined in their support of each other. For instance, imagining supported developing conjectures and conjectures led to new mental images.
In comparison, during another task, Amy confirmed she had no mental image and could not “visualise.” This was a significant difference between the tasks. Rather than providing images, structure and completed examples, I had relied on Amy already having imagery for number (which I did not assume with algebraic symbols) and being able to apply her mathematical powers to this imagery and previous learning. Instead, Amy’s lack of imagery for numbers apparently prevented mental manipulation and sense of what was occurring, while absence of completed examples meant time to stop and make sense of relationship was not encouraged in the same way. As my own method for the other activity had built on mental imagery, and an MGA approach, I may be imposing that as an ideal, but the algebra tile task showed mental (and physical) imagery was important in driving progression and would likely have been useful in the other case.
The main similarity in Amy’s response to the tasks was that generalities retained followed connections made herself, through mathematical powers. This was particularly true where Amy tried to verify inaccurate conjectures and became stuck before further specialising prompted accurate generalities of which Amy could convince herself. The algebra tile task’s generalities were the general nature of the tiles and symbols and equivalency of like symbols, the first of which was embedded by Amy creating her own examples and applying to new questions, the second building on Amy’s classification of tiles, transferring to symbols.
Amy’s enjoyment and recall from using her own powers to discover generality and creating her own examples supports the principle I followed, that learners gain most actively exercising their mathematical powers. Boaler (2009, p30), states that students need to “engage, do… problem solve” – acting as mathematicians to experience mathematics as “living”. However, some problem solving in other tasks left Amy feeling frustrated, due to little strategy or previous experience of problem solving. Christodoulou (2013, pp96-98) shows the pitfalls of expecting learners to behave like experts prior to conceptual understanding or, as Barton (2018, p300) points out, not knowing how to use it, while it is possible that inaccurate generalisations will occur and be internalised. The former was apparent in the less successful task where Amy showed seemingly limited conception of number and lack of strategies, until intervention provided tools for progress, which demonstrated my initial approach did not support her development. The latter was potential in both tasks, had I not provided or suggested new special cases. However, revising conjectures proved powerful for Amy, suggesting that creating and resolving conflict between initial ideas and new exposures deepens understanding, providing this does occur.
Although I felt the algebra tile task was successful, objections to my approach could be that imagery is provided instead of Amy building her own and that the structure is too closed, potentially causing behavioural rather than conceptual understanding. However, arguably providing some imagery is more important than leaving none. Willingam (2009, p88) avers, “we understand new things in the context of things we already know.” His recommendation of varied exposures suggests that images/manipulatives of varied forms, but same function, could improve grasp of abstraction. Even so, algebra tiles were powerful as a “mediating representational structure” (Bruner, 1966,p65) which could add to Amy’s imagery, something Bruner(p66) concluded was as important as a strong sense of underlying abstraction. This too, I believe answers concerns over behavioural instruction. Admittedly, red tiles do not logically delete corresponding ones in other contexts, but zero pairs are explicable, therefore if it is understood why the tiles are so used, they can mediate to activity and understanding, supporting concept as well as behaviour.
My experience of working with Amy throughout the module (and these tasks in particular) led me to believe that learners in early conceptual stages need empowering through structure, examples and imagery to make their own discoveries for effective development of algebraic thinking. However, opportunity must be created to reveal and challenge misconceptions.
References
Barton, C (2018) How I wish I’d taught mathematics. Woodbridge: John Catt Educational Ltd.
Boaler, J. (2009) The elephant in the classroom. London: Souvenir Press
Bruner, J (1966) Toward a theory of instruction. Cambridge, MA: Harvard University Press
Bruner, J (1986) Actual minds, possible worlds Cambridge, MA: Harvard University Press.
Christodoulou, D (2014) Seven Myths About Education Oxon: Routledge
Drury, H (2018) How to teach mathematics for mastery Oxford: Oxford University Press
Willingham, D (2009) Why don’t students like school? USA: Jossey Bass
Algebra tiles site: https://www.didax.com/apps/algebra-tiles/
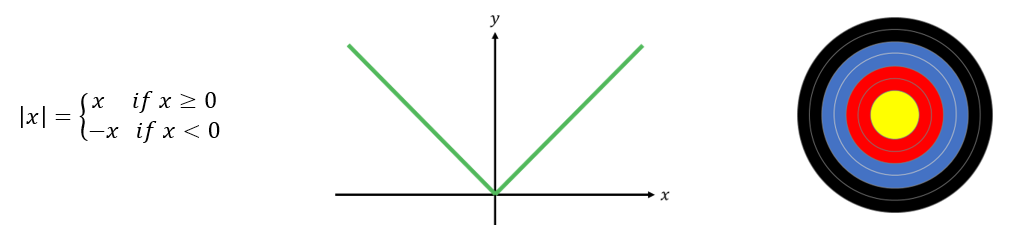
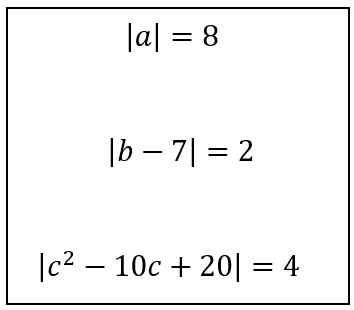 However, the second question can be solved using different approaches. Some learners rewrite it as two separate linear equations: either b – 7 = 2 or b – 7 = -2. Others instead think about it in terms of distance: which two numbers satisfy the statement “the distance between b and 7 on the number line is 2”? The third question is perhaps a little too complicated to think of in terms of distance, so it would probably be most efficient to rewrite this as two quadratic equations, but multiple representations can still help understanding; sketching a graph can help learners to appreciate why this equation can have up to four solutions.
However, the second question can be solved using different approaches. Some learners rewrite it as two separate linear equations: either b – 7 = 2 or b – 7 = -2. Others instead think about it in terms of distance: which two numbers satisfy the statement “the distance between b and 7 on the number line is 2”? The third question is perhaps a little too complicated to think of in terms of distance, so it would probably be most efficient to rewrite this as two quadratic equations, but multiple representations can still help understanding; sketching a graph can help learners to appreciate why this equation can have up to four solutions. This question might seem intimidating, but it is perhaps less so when it is reframed in terms of distance: “sketch all of the complex numbers which are a distance 2 away from the fixed point 1+2i ”. This gives a big clue as to the shape of the final answer, recalling the archery target.
This question might seem intimidating, but it is perhaps less so when it is reframed in terms of distance: “sketch all of the complex numbers which are a distance 2 away from the fixed point 1+2i ”. This gives a big clue as to the shape of the final answer, recalling the archery target.