This blog post was written by Roshani Senior, an OU mathematics graduate who undertook a 3 month virtual internship with the school of mathematics and statistics. Roshani’s placement was focused on developing external engagement materials based on mathematics.
In this blog post, Roshani writes about under represented voices in mathematics, which is a particular interest of hers. She reflects that as a school student of Indian origin, she learned about European mathematicians but it was not until she left school that she learned about the many contributions of Indian mathematicians. She believes that mathematics should be taught in an inclusive way, sharing the experiences and achievements of mathematicians from across different cultures.
This blog focuses on the contribution of two Indian mathematicians to the concept of zero.

Aryabhata

Brahmagupta
The move from zero as merely a placeholder by the Mayans and Babylonians – a tool to distinguish larger numbers from smaller ones to a digit of its own was established in India by a man named Aryabhata in the 5th Century. A mathematician and astronomer, Aryabhata contributed multiple mathematical concepts, crucial to maths as we know it today, including the value of pi being 3.14 and the formula for a right-angled triangle. The prior absence of zero created difficulty in carrying out simple calculations.
Gwalior, India
Following this in the 7th century a man known as Brahmagupta, developed the earliest known methods for using zero within calculations, treating it as a number for the first time. The use of zero was inscribed on the walls of the Chaturbhuj temple in Gwalior, India. Carved into a wall the numbers 270 and 50 can be seen today and have been established as the second oldest recorded zeros in history. The city of Gwalior was designed so that the gardens around the temple were large enough so that each day the gardens would produce enough flowers to create 50 garlands for the employees of the temple. When the temple was built this was inscribed on the walls and it is this 50 that can be seen, annotated almost as we would write it today. 
What we now call zero in English, Brahmagupta named “shunya” or “sunya”, the Sanskrit word for emptiness or nothingness.
Aryabhata and Brahmagupta wrote their works in Sanskrit, an ancient and classical language of India. Their use of numbers would have looked quite different to what we use in English now. However, Sanskrit had a large
influence in how the English numeric system is written and so there are quite a lot of similarities.
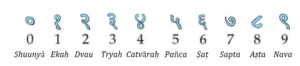
Numbers 0 to 9 in Sanskrit
Within Indian culture there is an idea of one having a “nothing” or a void inside of yourself. Long before the conception of zero as a digit, this philosophical concept was taught within Hinduism and Buddhism and practised through meditation. The ancient Hindu symbol, the “Bindi” or “Bindu”, a circle with a dot in the centre symbolised this and was what probably led to the use of an oval as the symbol for the Sunya. It has been suggested that this cultural and philosophical influence on the concept of zero is what allowed India to develop what previous civilizations did not think of.
Brahmagupta was also the first to demonstrate that zero can be reached through calculation. He wrote these rules in his book the “Brahmasphutasiddhanta”. He was therefore able to make another important leap – in the creation of negative numbers, which he initially called “debts”. Brahmagupta placed small dots above numbers to indicate they were negative, unlike today where a minus symbol is used. The use of negative numbers was shown in “Brahmasphutasiddhanta”. Brahmagupta also demonstrated their use to produce the quadratic formula. and demonstrated rules for calculations involving both negative numbers and zero.
His rules were as follows:
Addition and Subtraction with zero and negative numbers:
- When zero is added to a number or subtracted from a number, the number remains unchanged; and a number multiplied by zero becomes zero.
- A debt minus zero is a debt.
- A fortune minus zero is a fortune.
Zero minus zero is a zero. - A debt subtracted from zero is a fortune.
- A fortune subtracted from zero is a debt.
Division and multiplication with zero and negative numbers:
- Positive or negative numbers when divided by zero is a fraction with zero as denominator.
- Zero divided by negative or positive numbers is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator.
- Zero divided by zero is zero.
- The product of zero and a debt or fortune is zero.
- The product of zero and zero is zero.
The product or quotient of two fortunes is one fortune. - The product or quotient of two debts is one fortune.
- The product or quotient of a debt and a fortune is a debt.
- The product or quotient of a fortune and a debt is a debt.
When Brahmagupta attempted to divide 0 by 0, he came to the result of 0. However, most modern mathematicians would argue that 0 divided by 0 is undefined, or an “indeterminate form”. Despite this outlier, the rest of Brahmagupta’s grasp on the number zero is exactly how we conceptualize it today.
The concept of zero gradually moved East into China. Then West to reach the Middle East. And finally, over half a century from its conception, the zero made it to Europe, where its importance was finally recognised by the Western culture that previously frowned on the idea of nothing, referring to it as meaningless or even satanic. In 1200 AD, Italian mathematician Fibonacci, a man who has been considered the ‘most talented western mathematician of the middle ages’ wrote of Indian Mathematics and their use of zero:

Despite the number zero having quite literally no value, its concept has allowed mathematics to develop into what it is today. Its curation led to the three pillars of modern mathematics: algebra, algorithms, and calculus. The use of calculus (the mathematical study of continuous change), which the zero is crucial for, has allowed engineering and modern technology to be possible. The use of zero and one within the binary system is what made computing possible. So, without the invention of zero much of what we know today would not have been possible. The device you are reading this on would not have been able to be invented, if not for Aryabhata, Brahmagupta and India’s fascination with the idea of nothing.
