… even if you don’t get to a solution you’ll learn more about the environment around you
What makes some people love doing maths and others not? This is a question that inspires our research at the OU? We are always looking for stories of people who have come to maths in a surprising way. In this blog we talk to Charlotte, who spent primary school struggling with times tables and calculations, and is now finishing her mathematics degree at Murray Edwards College in Cambridge. She reflects on how her dyslexia influences the way she approaches maths.

There are some points of Charlotte’s story that resonate with mathematics education research:
- There is more than one way to do well in maths: you can be the person who sees connections, or a careful symbol-cruncher;
- It’s very common to feel that you are struggling in maths, and not notice where you are succeeding (especially for quieter, slower workers);
- Persistence – doing the same thing – is over-rated in mathematics; being willing to try another way is more successful;
- Families and stories of people doing maths (even simple maths) are powerful motivators
Here is what Charlotte told us:
My earliest memories of doing maths involve me walking to primary school with my mum and trying to recite timestables. I was awful at timestables and at no point did I believe I could ever learn them, even with mum’s chants. I think she gave up quite quickly. I also remember being taught how to read analogue clocks in maths lessons. I could never do that either (although now I prefer them to digital).
Looking back the thing I found difficult was anything involving memory and/or calculations. That is pretty much everything in primary school. A particular memory that has stayed with me was during secondary school when I was 14. When we finished a lesson early we always did the same thing: we had specific numbers and operations and had to make every number up to 100 with them. Whenever we went back to it the boy next to me would laugh at how slow I was compared to everyone else, so that eventually I gave up and refused to participate. I dreaded maths lesson that entire year because of this.
My primary school split us into two maths sets. I was in the top one, but I couldn’t keep up. At secondary school I was put in the second set of five, but I found it very difficult and did not feel like I belonged. Everyone seemed to be faster than me.
That did change. I remember the first time I finished a task first; the teacher came over to check my answers and started to show me the best strategy to use. Then we realised I had already used that strategy. It was a very good feeling.
Right at the end of year 9, just before the sets were locked for GCSEs, I was moved into the top set. Again I started near the bottom, but slowly moved up and was eventually the best girl in the set (not too hard-there were only 4 of us in a class of 30). This pattern repeated again in sixth form when I moved to a new (all girls) school; at the start I felt like everyone knew things I didn’t, but by the end I could correct the teacher.
I can see now that as I got older I got much better at maths compared to my peers; I think this reflects the change in maths from computation to more abstract concepts. I was planning on doing either a Physics or Computer Science degree until I did A level maths; this is when you start getting close to the fun stuff.
Also, I was diagnosed with dyslexia in year 12, when a teacher from my new school told me to get tested. My dyslexia still affects my maths a lot; My short term memory is very bad and I misread and/or mix up symbols in equations. This makes tasks like finding eigenvalues and simplifying equations literally impossible for me, when other people find it simple. I can’t describe how annoying it is to solve a ‘trivial’ equation five times and get five different answers. I have had to avoid as many courses as I could which involve this sort of algebra, which has naturally pushed me to more abstract and pure maths.
I don’t spend all my time at university working. I love playing rugby; it’s such a great balance between tactical thinking and physical strength. Also my dad loves it so it’s in the family! 
I played for the Cambridge 1st team and was in the winning Twickenham squad last December, but sadly I am not playing rugby this term as I need to focus on my studies. I plan on going back to it once I’ve graduated.
I also spend a lot of time with CUBB, the university brass band and I’m the concert manager this year. The friends I have made at CUBB have been some of the best people I’ve ever met, and I suspect they will be life long.
What I am hoping to do next is a Computational Biology masters, so that I can carry on studying maths, but start using it in a more practical way. We can learn so much about humans, plants and animals by studying their DNA and that is about finding mathematical patterns in data. The computers do all the computation for me. Afterwards I’d maybe like to go onto a PhD and work in bioinformatics.
We asked Charlotte is she had any messages for others about learning maths, which she did, and she also has a Milton Keynes connection …
First message is that primary school/GCSE maths is ugly and boring; it gets so much better after that. It does also get harder though, which brings me to my next message. So much of maths is having the confidence to follow your intuition and try a solution, especially at the higher level (A-levels and beyond). Starting a difficult maths questions is often like exploring a dark pit; you have no idea what’s around you, so it’s easy to give up, but you just need to try things; even if you don’t get to a solution you’ll learn more about the environment around you so that your next attempt will be better. Maths is not about getting the solution (at least it isn’t when you get to the good stuff), it’s about exploring a weird abstract thing, and that is really fun. For example, I love to think about countability. It is fascinating that there are ‘more’ real numbers (decimals) squashed between 0 and 1 than there are whole numbers in total. (Read more here).
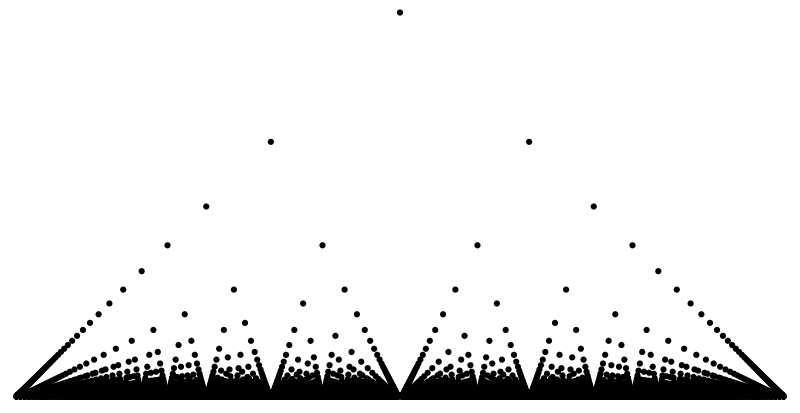
A way of ordering the fractions between 0 and 1, but not the irrationals: the Calkin-Wilf tree
The final thing I’ll mention played a vital part in me deciding to apply for a maths degree in the first place. Bletchley Park is where codes were broken in the second world war by a bunch of mathematicians, and is where modern computation was invented. I didn’t really understand the machines back when I first visited but just the idea of them made me very excited, and I go often go back there with my family to this day.
