Developing Thinking in Learning and Doing Geometry.
You might have thought the title of this blog is unnecessarily complicated! It is a hybrid of the names for the current Open University geometry module (Developing Thinking in Geometry) and the new geometry module (Learning and Doing Geometry) which is currently being written by the Mathematics Education team at the OU. This blog post is about our developing thinking of how people learn and do geometry.
The current module
Developing Thinking in Geometry was one of a suite of modules originally developed as part of a post-graduate diploma for practising teachers and launched in 2005. It is now fifteen years old and is studied by level three undergraduate students, many but not all of whom intend to enter the teaching profession. The time has come to replace it with a new module written for contemporary students. When writing the module materials our picture of one typical student is of someone preparing to undertake PGCE in Secondary Mathematics or in Primary teaching. Other students may be working as teaching assistants or as unqualified teachers of mathematics who wish to upskill in the areas of mathematics subject knowledge and pedagogy. Other students may simply be interested in learning about learning and acquiring the specific skillset which allows them to do this.
 The textbook which forms the basis of the study materials for the current module. |
The production of the new module
The process of developing a new module for the Open University typically takes two years. The writing team have spent the last academic year writing the content of 30 weeks of study at 10 hours per week for this 30 credit module. Once this is completed, and has been reviewed by our critical readers, there is still a lot of work to be done in the second year as the module is gradually uploaded to the website; editing, production of high specification graphics, and videos, building the interactive content being amongst those. That’s not to mention the work done by people in the rights teams and the library to ensure we give students access to third party material and literature. All of this is being co-ordinated by our curriculum manager and the learning design team. Last but not least our External Assessor will oversee the materials to check that they are consistent with the standards of level 6 study (equivalent to OU third level undergraduate studies) in the Higher Education sector.
In writing Learning and Doing Geometry we aim to keep much of the theoretical underpinning of the older module but target it to the contemporary student demographic and move all resources online, with the exception of the task booklets. Important aspects of the module include the explicit connections made between presentation of pedagogic theories and their application to learner activities. Important ideas from selected theories in the field of mathematics education have been included in the module materials. Students studying Learning and Doing Geometry will learn about how geometric thinking develops.
Developing thinking about learning
Students studying the module will be asked to work on geometric tasks and to reflect on their own learning and their approaches to solving problems by making reference to a set of important module ideas. This aspect of the module is clearly important because the only mind you can look inside is your own. Being aware of how you learn and the approaches which work for you and linking them to important module ideas requires a degree of self-awareness and objectivity. The activity of thinking about your mental processes is known as meta-cognition and is considered to be the highest level of thinking. Students can use the insight gained from observing and reflecting on their own learning as a guide to ascertain how other learners learn geometry, whether this is in the context of the classroom or in smaller groups. It is important to be aware that not all people learn in the same way and that less experienced learners often need to work at a slower pace while they assimilate new knowledge and skills. Careful observation and listening to what they say are the best ways to explore how learners may be thinking about the geometry. Use of questions to prompt learners to talk about what they are doing and how they are thinking can shed more light onto their thought processes. It is the closest that you can get to looking into the mind of another person.
Perceptual and discursive reasoning
In order to reflect on geometric reasoning. we have identified important ideas and described how these can be used to support the analysis of learning and doing geometry. Two of the most important of these ideas in the context of geometry are perceptual reasoning and discursive reasoning. At the simplest level these two ideas describe how learners look at geometric figures and how they think and talk about them. Of course, it is more complex than that. When learners look at geometric figures they may notice all kinds of different aspects of the figure, emphasising what appear to be the important features and ignoring others. Learners may divide the figure into constituent parts and might imagine what happens if changes are made to it. When learners articulate aspects of the same geometric figure they may describe what they have noticed, attempt to justify this or ask questions about the figure.
Invariance and change
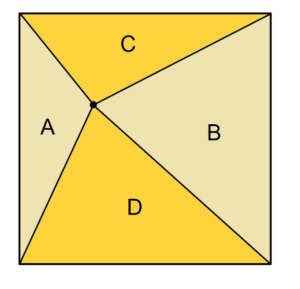
Another important idea in geometry is invariance and change. This idea can be used as a strategy by students to notice what is the same and what is different between two different figures, or two examples of the same figure. Students can notice what stays the same and what changes when they act on a figure, for example if the figure has been constructed in a dynamic geometry software program. The ability to identify invariance and change in geometry draws on learners’ natural tendency to spot differences and look for patterns and this gives it its power for learning. The example below demonstrates a typical task from the module where observing invariance and change can be used to as an approach.
Point SquarePlace a point in a square as shown. Investigate areas A, B, C and D. What happens as the point moves?
|
This task, which is taken from one of the task booklets for Learning and Doing geometry, looks like a simple question. It becomes much more interesting as the learner begins to explore the areas A, B, C and D and to observe what happens to those areas as the point moves. Consider how perceptual and discursive reasoning come into play. How does asking ‘what is the same and what is different’ help the learner to notice invariance and change as the point moves? |
Representations
Representations of geometric figures is another idea which is important in the module. In geometry we always work with representations, whether that be static diagrams drawn on paper, dynamic figures on the computer screen, or a worded definition of a figure. The type of representation and the context of the representation are important factors which influence the way that learners think and reason about the geometric objects being represented.
Content of the new module
These and other module ideas form a framework for students to reflect on their own geometric reasoning and to analyse the reasoning of learners which they work with. Other important theories that have arisen from research into mathematics education are presented in the module. We have aimed to provide an up-to-date picture of current educational know-how. Curriculum is mentioned briefly, but we are aware that the Mathematics Education modules are studied by students in England, Scotland, Wales, Northern Ireland and Ireland as well as by international students. There is a range of curricula in the various jurisdictions but most of the mathematics content is typical across them all. The mathematics content is presented at the level of secondary education for ages 11 to 18. What makes Learning and Doing Geometry and the other Mathematics Education modules into OU level three material is the depth and complexity of the Educational theory.