Here in the OU Maths Education department we have been having some interesting discussions about the specific words we use when talking about teaching practice. In this post we discuss the variety of ways in which examples are used in mathematics teaching, either consciously or unconsciously.
As teachers, we use examples all the time – it is almost impossible to help someone learn a new concept without giving an example on which to hang it. Without examples, the mathematics, the definition or the concept is abstract – there’s nothing to see, touch or do, and we often can’t really tell whether it’s true or makes sense.
Here are some of the ways in which examples are used in classrooms. Thinking about them explicitly can help us to check we are making the best use of examples as a tool for understanding. (In a truly meta mode, we give examples of each type of example).
Modelling examples
These are the classic ‘Worked examples’ where a process or procedure is modelled to students so they can see it in action. For example, working through an application of the quadratic formula, using numbers instead of a, b and c.
Particular examples / specific examples
A particular example (sometimes referred to as specific example or specific case) is a single example where any generality has been removed. It can be used to illustrate a more general definition or concept. For example, a 3 × 3 square is a specific example of the more general class of squares. In the literature we sometimes see ‘special’ used in a similar way, since every object is special somehow. This means it is sometimes confused with ‘special cases’ or ‘special kinds’.
Special cases / special kinds
Special cases are those lovely examples that can sometimes catch us out and lead us to believe processes always ‘work’ (for example factorising only works for special kinds of quadratic equations). Special cases have interesting properties or additional constraints applied to them, and so we can view special cases as a subset or subclass of a larger set or class. For example, in Geometry, the squares are a special kind of rectangle. In Number theory, 2 is a special case of the prime numbers.
Peculiar examples
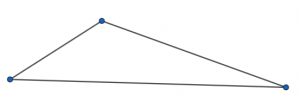
Peculiar examples are those particular or specific examples where something interesting or unusual is happening. Let’s use the example of a dynamic triangle, where all the vertices can be manipulated.
You could drag one vertex so close to the opposite side that the triangle looks almost like a straight line but is, in fact, a very thin triangle. This type of peculiar example is sometimes called a degenerate example.
Another way of manipulating a triangle is to drag a vertex so that the triangle is isosceles. Of course what is ‘peculiar’ to one person might not be to another; it depends what examples each person considers as part of their concept image (Vinner and Tall, 1981).
Non-examples
These are brilliantly useful and often underused. Even outside of mathematics, it is sometimes clearer to define what something isn’t than what something is. Non-examples deliberately do not hold certain properties or do not meet required definitions, so looking at non-examples serves to clarify the boundaries of a concept or a definition (Bills et al., 2006) . Non-examples are most useful when presented alongside specific or particular examples, because we can see the contrast clearly.
Here are some examples and non-examples of polygons: A closed plane shape with straight sides.
Generic examples
A generic example is a specific example that is used to illustrate steps of reasoning that hold for the general case. The generic example is an object that is not there in its own right, but as a characteristic representative of the class. We often use these without thinking about it, e.g. we might draw a 3 by 4 rectangle and say it has 3 rows of 4 unit squares so its area is 12, and take that as a proof that this is the area formula for any rectangle. We have not actually reasoned with a general rectangle, but with a specific one that takes the role of a generic example. To turn it in to a formal proof, we need to be sure that the same reasoning could be adapted to work with any rectangle. Reasoning with a generic example works when there are no peculiar cases to take into account. It is useful to do when it reduces abstraction for learners.
Counter-examples
Not to be confused with non-examples, counter-examples are mainly used when working with theorems, conjectures and proofs. They are specific cases for which a conjecture does not hold true and, as such, counter-examples may refer to special cases. For example, a counter-example for the often-held belief that all prime numbers are odd can be found in the prime number 2, which is even.
A counter-example for the conjecture that only quadrilaterals with line symmetry can be split into two congruent triangles is a parallelogram, which has rotational symmetry.
We hope you’ve enjoyed thinking explicitly about examples. If you have any questions or comments you’d like to share about your own experience of using examples, please use the comment space below.
References
Bills, L., Dreyfus, T., Mason, J., Tsamir, P., Watson, A. & Zaslavsky, O. (2006). Exemplification in Mathematics Education. In J. Novotna (Ed.), Proceedings of the 30th Conference of the International Group for the Psychology of Mathematics Education. Prague, Czech Republic: PME.
Vinner, S., and Tall, D. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity, Educational studies in mathematics, 12(2), pp. 151-169