This post is written, in both English and Welsh, by Dr Delyth Tomos, an OU Associate Lecturer who tutors on modules in mathematics and statistics, and engineering.
Delyth has recently co-led a project looking at Welsh-medium tuition in mathematics. To learn more about the project, click here
Ysgrifennwyd y neges hon, yn y Gymraeg ac yn Saesneg, gan Dr Delyth Tomos, Darlithydd Cyswllt gyda’r Brifysgol Agored, sy’n diwtor ar fodiwlau mewn mathemateg ac ystadegau, a pheirianneg.
Yn ddiweddar mae Delyth wedi cyd-arwain prosiect yn edrych ar addysgu mathemateg drwy gyfrwng y Gymraeg. Er mwyn gweld mwy o wybodaeth am y prosiect, cliciwch yma.
As someone who has lived and worked in North Wales since birth, being exposed to two languages, Cymraeg/Welsh and English, is pretty much a way of life. Children are taught in both languages from an early age, and develop linguistic skills that allow them to participate fully in education, work, family and social activities in two languages, thus maximising the opportunities available to them. Discussions in formal and informal settings are frequently conducted through both languages, switching from one to the other, and most of us do this with ease, hardly realising that what we are doing is much more complicated linguistically than we possibly realise.

Welsh landscape. Image credit David Kjaer / Nature Picture Library / Universal Images Group.
A bilingual education involves subjects being taught in both languages, and effective strategies have evolved over the decades, underpinned by a wealth of research in countries where living through the medium of more than one language is the norm (Spitzer, 2016 and Mukan et al, 2017). These strategies promote constructive learning where the use of two languages enhances a learner’s resilience and effectiveness within specific subjects as well as their language skills in general.
Learning mathematics through the medium of both Cymraeg and English encourages learners to acquire and develop flexible approaches to their studies. Understanding and learning how to solve mathematical problems requires a learner to develop a subject-specific vocabulary which needs to be incorporated within the learner’s wider language skills. In mathematics, a learner needs to be able to describe and interpret a problem, analyse and select relevant pieces of information from a given situation, organise the information, consider how this information may be used to address a particular problem, select and justify suitable mathematical methods, undertake various mathematical calculations and manipulations, and finally, to interpret their solutions or results in order to address the original problem. It is clear that these strategies are complex, and it can also be seen that most of these skills are deeply embedded in language.

School sign in English and Welsh languages. Image credit David Hunter / Robert Harding World Imagery / Universal Images Group
When discussing mathematical concepts and terms in different languages, learners have opportunities to make connections with previous knowledge in both languages, and this, in turn helps them to construct their learning of mathematical ideas in both languages. Mathematical problems may be described and framed in a similar manner in two different languages, but the translation will not be exactly the same. Translation is not a matter of substituting one word from one language to an equal term in another language. Effective translation requires an equivalent adaptation of meaning in both languages in addition to syntactic flexibility and choosing suitable terms to delineate a problem in a manner that is accurate and helpful. Being creative and flexible as part of the translation process results in mathematical problems being conceptualized from two slightly different directions, resulting in a deeper understanding of how to address problems.
Learning mathematics (and other subjects) through the medium of two languages thus provides learners with opportunities to fully engage in learning, in both their first and second language, and to engage with concepts from two slightly different directions. This in turn encourages them to become flexible, creative and resilient learners and this naturally benefits mathematics learners.
Manteision astudio mathemateg mewn dwy iaith (Cymraeg a Saesneg)
Fel rhywun sydd wedi byw a gweithio yng Ngogledd Cymru ers ei geni, mae dod i gysylltiad â dwy iaith, Cymraeg a Saesneg, yn ffordd o fyw. Caiff plant eu haddysgu yn y ddwy iaith o oedran cynnar, a byddant un datblygu sgiliau ieithyddol sy’n caniatáu iddynt gymryd rhan lawn mewn addysg, gwaith, gweithgareddau teuluol a chymdeithasol mewn dwy iaith, gan wneud y mwyaf o’r cyfleoedd sydd ar gael iddynt. Caiff trafodaethau mewn sefyllfaoedd ffurfiol ac anffurfiol eu cynnal yn aml drwy’r ddwy iaith, gan newid o’r naill i’r llall, ac mae’r rhan fwyaf ohonom yn gwneud hyn yn rhwydd, prin yn sylweddoli bod yr hyn yr ydym yn ei wneud yn llawer mwy cymhleth yn ieithyddol nag yr ydym o bosibl yn sylweddoli.

tirwedd Cymru. Credyd delwedd David Kjaer / Llyfrgell Lluniau Natur / Grŵp Delweddau Cyffredinol.
Mae addysg ddwyieithog yn golygu bod pynciau’n cael eu haddysgu yn y ddwy iaith, ac mae strategaethau effeithiol wedi datblygu dros y degawdau, wedi’u hategu gan gyfoeth o ymchwil mewn gwledydd lle mae byw trwy gyfrwng mwy nag un iaith yn norm. (Spitzer, 2016 A Mukan et al, 2017). Mae’r strategaethau hyn yn hybu dysgu adeiladol lle mae’r defnydd o ddwy iaith yn gwella gwydnwch ac effeithiolrwydd dysgwr o fewn pynciau penodol yn ogystal â’u sgiliau iaith.
Mae dysgu mathemateg trwy gyfrwng y Gymraeg a’r Saesneg yn annog dysgwyr i gaffael a datblygu ymagweddau hyblyg at eu hastudiaethau. Mae deall a dysgu sut i ddatrys problemau mathemategol angen i ddysgwr ddatblygu geirfa pwnc-benodol y mae angen ei hymgorffori o fewn sgiliau iaith ehangach y dysgwr. Mae angen i’r dysgwr allu disgrifio a dehongli problem, dadansoddi a dewis darnau perthnasol o wybodaeth o sefyllfa benodol, trefnu’r wybodaeth, ystyried sut y gellir defnyddio’r wybodaeth hon i fynd i’r afael â phroblem benodol, dewis a chyfiawnhau dulliau mathemategol addas, gwneud cyfrifiadau a thriniadau mathemategol amrywiol, ac yn olaf, dehongli eu hatebion neu ganlyniadau er mwyn mynd i’r afael â’r broblem wreiddiol. Mae’n amlwg bod y strategaethau hyn yn gymhleth, a gellir gweld hefyd bod y rhan fwyaf o’r sgiliau hyn wedi’u gwreiddio’n ddwfn mewn iaith.

Arwyddion ysgol yn y Gymraeg a’r Saesneg. Credyd delwedd David Hunter / Robert Harding World Imagery / Grŵp Delweddau Cyffredinol.
Wrth drafod cysyniadau a thermau mathemategol mewn gwahanol ieithoedd, caiff dysgwyr gyfleoedd i wneud cysylltiadau â gwybodaeth flaenorol yn y ddwy iaith, ac mae hyn, yn ei dro, yn eu helpu i adeiladu eu dysgu o syniadau mathemategol yn y ddwy iaith. Gellir disgrifio problemau mathemategol a’u fframio mewn modd tebyg mewn dwy iaith wahanol, ond ni fydd y cyfieithiad yn union yr un fath. Nid yw cyfieithu yn fater o amnewid un gair o un iaith i derm cyfartal mewn iaith arall. Mae cyfieithu effeithiol yn gofyn am addasiad cyfatebol o ystyr yn y ddwy iaith yn ogystal â hyblygrwydd cystrawennol a dewis termau addas i amlinellu problem mewn modd sy’n gywir ac yn ddefnyddiol. Mae bod yn greadigol a hyblyg fel rhan o’r broses gyfieithu yn arwain at gysyniadoli problemau mathemategol o ddau gyfeiriad ychydig yn wahanol, gan arwain at ddealltwriaeth ddyfnach o sut i fynd i’r afael â phroblemau.
Mae dysgu mathemateg (a phynciau eraill) trwy gyfrwng dwy iaith felly yn rhoi cyfleoedd i ddysgwyr ymgysylltu’n llawn â dysgu, yn eu hiaith gyntaf a’u hail iaith, ac i ymgysylltu â chysyniadau o ddau gyfeiriad ychydig yn wahanol. Mae hyn yn ei dro yn eu hannog i ddod yn ddysgwyr hyblyg, creadigol a gwydn, ac mae manteision amlwg i hyn ar gyfer dysgwyr mathemateg.
References/Cyfeiriadau
Mukan, N. et al (2017). The Development of Bilingual Education in Canada. Advanced Education, Issue 4(8) pp. 35 – 40.
Mukan, N. et al (2017). Datblygiad Addysg Ddwyieithog yng Nghanada. Addysg Uwch, Rhifyn 4(8) tt. 35 – 40.
Spitzer, M (2016). Bilingual Benefits in Education and Health. Trends in Neuroscience and Education, Volume 5, Issue 2, pp 67-76.
Spitzer, M (2016). Buddion Dwyieithog mewn Addysg ac Iechyd. Tueddiadau mewn Niwrowyddoniaeth ac Addysg, Cyfrol 5, Rhifyn 2, tt 67-76.



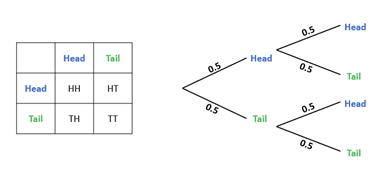
 I mentioned that she need not give exact values, only its relation to the other car, for example, ‘Car A is older than B.’ She used this language when reasoning her responses to the statements. For statement (a)(i), she answered ‘False, car B is more expensive because it is younger.’ I re-phrased the question to, ‘Ignoring age, which car is more expensive?’ (I will elaborate why later, but I wanted her to practise using the y-axis.) She finished the remaining statements without much difficulty and gave good descriptions of the cars that I recorded.
I mentioned that she need not give exact values, only its relation to the other car, for example, ‘Car A is older than B.’ She used this language when reasoning her responses to the statements. For statement (a)(i), she answered ‘False, car B is more expensive because it is younger.’ I re-phrased the question to, ‘Ignoring age, which car is more expensive?’ (I will elaborate why later, but I wanted her to practise using the y-axis.) She finished the remaining statements without much difficulty and gave good descriptions of the cars that I recorded.











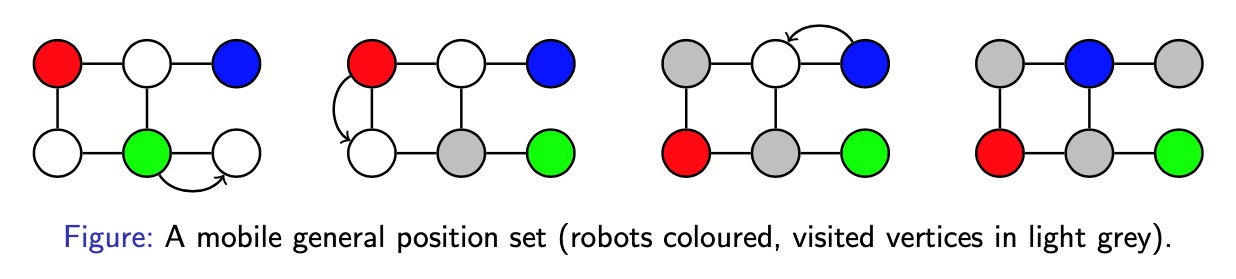










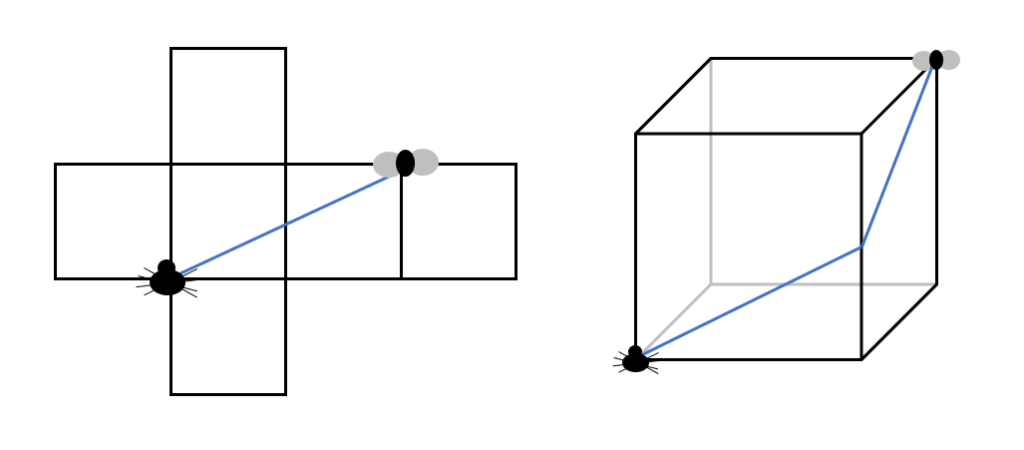
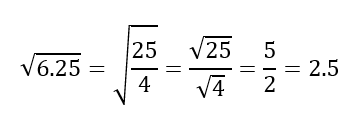
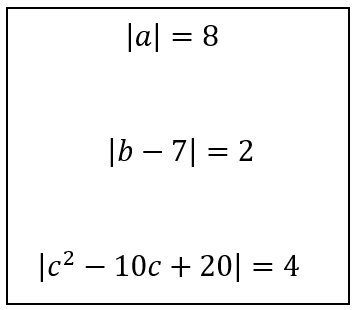 However, the second question can be solved using different approaches. Some learners rewrite it as two separate linear equations: either b – 7 = 2 or b – 7 = -2. Others instead think about it in terms of distance: which two numbers satisfy the statement “the distance between b and 7 on the number line is 2”? The third question is perhaps a little too complicated to think of in terms of distance, so it would probably be most efficient to rewrite this as two quadratic equations, but multiple representations can still help understanding; sketching a graph can help learners to appreciate why this equation can have up to four solutions.
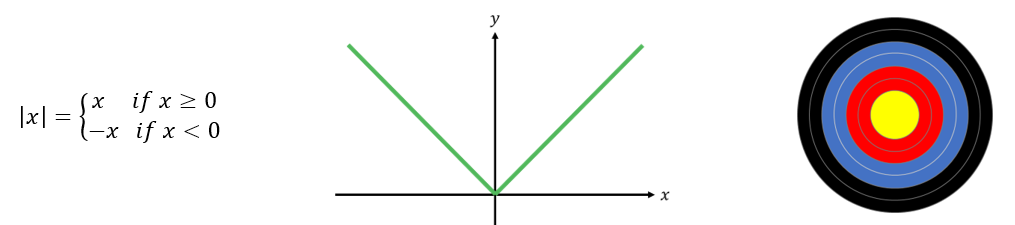
However, the second question can be solved using different approaches. Some learners rewrite it as two separate linear equations: either b – 7 = 2 or b – 7 = -2. Others instead think about it in terms of distance: which two numbers satisfy the statement “the distance between b and 7 on the number line is 2”? The third question is perhaps a little too complicated to think of in terms of distance, so it would probably be most efficient to rewrite this as two quadratic equations, but multiple representations can still help understanding; sketching a graph can help learners to appreciate why this equation can have up to four solutions. This question might seem intimidating, but it is perhaps less so when it is reframed in terms of distance: “sketch all of the complex numbers which are a distance 2 away from the fixed point 1+2i ”. This gives a big clue as to the shape of the final answer, recalling the archery target.
This question might seem intimidating, but it is perhaps less so when it is reframed in terms of distance: “sketch all of the complex numbers which are a distance 2 away from the fixed point 1+2i ”. This gives a big clue as to the shape of the final answer, recalling the archery target.