As an extension to my daughter Helen’s iCMA statistics project, random guess scores were calculated for multiple choice, multiple response and drag and drop questions in a number of different situations (e.g. with different numbers of attempts, different scoring algorithms, different numbers of options to select from and different numbers of options being correct, students being told how many options were correct, or not).
The random guess score for a question is essentially the score that you would expect from someone who is completely logical in working though the question but knows absolutely nothing about the subject matter.
Helen’s report is here.
Examples
Consider a multiple choice question in which the user has to select one from four options and has a single attempt. They have a one in four chance of getting the right answer, so the random guess score is 25%.
Now consider the same multiple choice question, but allow the user 4 attempts, with full marks available whenever the user gets the correct answer. The logical user can work through the responses in order, so will always get the correct answer within the four allowed attempts i.e. the random guess score is 100%.
Now consider the same multiple choice question, again with 4 attempts, but now the user scores 4 marks (100%) if they are correct at first attempt, 3 marks (75%) if correct at second attempt, 2 marks (50%) if correct at third attempt and 1 mark (25%) if correct at fourth attempt:
At the first attempt, as with example 1 the user has a 1 in 4 chance of getting the question right, and if they get it right at this attempt then they score 4.
In order to get a mark at the second attempt, the user has to get the question wrong at the first attempt. They have a 3 in 4 chance of doing this. Then they have a 1 in 3 chance of getting the question right, and if they get it right at this attempt then they score 3.
In order to get a mark at the third attempt, the user has to get the question wrong at the first attempt (probability 3/4) and the second attempt (probability 2/3). Then they have a 1/2 chance of getting the question right, and if they get it right at this attempt then they score 2.
In order to get a mark at the fourth attempt, the user has to get the question wrong at the first attempt (probability 3/4), the second attempt (probability 2/3) and the third attempt (probability 1/2). However they are then certain to get this question right, i.e. they have a probability of 1 of doing this, and if they get it right at this attempt then they score 1.
This means that the overall random guess score out of 4 is:
This is 62.5%.
Calculated values of random guess scores for a range of iCMA question types
Spreadsheets are available (below) giving random guess scores for various types of multiple choice, multiple response and drag and drop questions. However there are many variables that can influence the random guess score, so a random guess score calculator is also provided.
Multiple choice and multiple response questions
multiple_response_1 contains data for multiple choice and multiple response questions where students who get the answer wrong are simply told that their answer is incorrect. multiple_response_2 contains data for multiple choice and multiple response questions where students are told how many of their initial choices were correct.
In both cases, there are separate tabs for different total numbers of options. Under each tab the rows represent the number of correct options and the columns represent the number of attempts available. The upper table under each tab is for situations where users have been told how many options to select; the lower table is for when they have not been told how many options to select.
Drag and drop questions
drag_and_drop_once_only contains data for drag and drop questions where each draggable object may be put into at most one box. drag_and_drop_unlimited contains data for drag and drop questions where each draggable object may be put into an unlimited number of boxes.
In both cases, there are separate tabs for different numbers of boxes to be filled in. The rows represent the number of choices to put in the boxes and the columns show the number of attempts allowed. These figures assume that if a student does not get the question right then they are told how many of their choices are correct. If this assumption is not valid, the random guess score calculator should be used.
Random guess score calculator
To run the program:
- Unzip the folder RGS_calc
- Open a command prompt and navigate to the folder RGS_calc
- Type RGS_calc.exe into the command prompt
- Follow the onscreen instructions
An example of a surprising result
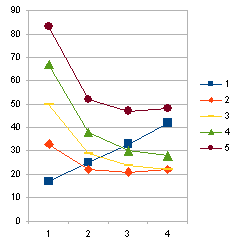
The way in which the random guess score varies with different factors is sometimes surprising and counterintuitive. For example, the figure below shows the variation of random guess score for a multiple response question with 6 options, in which the score available at each attempt falls proportionally and in which partial credit is given for answers that are partially correct at the final attempt. When only one option is required, the random guess score increases with number of attempts allowed. However, when more than one option is correct, the random guess score decreases with the number of attempts allowed.
This surprising result appears to be a consequence of giving partial credit for partially correct responses. If a completely correct final answer is required, the random guess score is dramatically reduced in some cases.

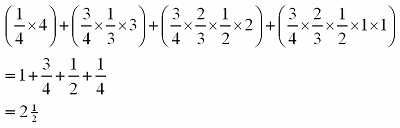
Dear Sally,
This post of yours has been on my list to respond to for quite some time now.
Two years ago I also developed Excel files with random guess scores for various question types. Not in relation to multiple attempts, but also when applied in summative exams to calculate the relative P-value of questions (P’=P-randomguessscore) and, using those, the lowest score for which a student receives a score of 1 (in the Netherlands we use a 10 point grading scale) representing the random guess score for the test as a whole.
Helen’s report at least is written by a statistics expert (I worked with trial and error) and I love it.
I would like to share my excel in this post or with Helen and write some more about this. Maybe I will put something up in my own blog.
Kind regards,
Silvester
Pingback: e-assessment (f)or learning » Blog Archive » Distractors for multiple-choice questions