Problems with fractions

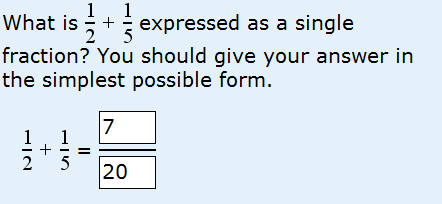
I’ve been aware for some time that Open University science students have problems with fractions (and many things that express themselves as difficulties in other areas e.g. working out units, simplifying algebraic expressions, have their origins in poor understanding of the arithmetic of fractions). We’ve improved our teaching all over the place, but I have recently become aware of a problem I hadn’t spotted before. Why do students give the (incorrect) answer shown below?

It’s actually remarkably simple – and once again the teaching material that I wrote ten years ago is not as clear as it might be. I was aware at that time that the most common mistake that students made when adding fractions was to add the numerators and denominators separately, so I rammed home the importance of finding a common denominator. So students find a common denominator (10) and then express each of the fractions to be added in terms of the common denominator: 5/10 + 2/10. Then they add the numerator and denominator separately to give 7/20. ARGHHH! The correct answer of course is 7/10. I’ve added a bit more explanation to our teaching text.

The other big problem with fractions concerns reciprocation and reciprocation of reciprocation. So students may know that

 x^-2=1/x²

but they don’t automatically appreciate that this means that

1/x^-2=x²

 I’ve improved the teaching on this. At a more basic level (but the problem is related) we have a question where students are asked to combine and rearrange two equations, giving their answer in the simplest possible form. The correct answer is 2ms/t². But we got quite a lot of answers in the form ms/t²/2. Oh dear.