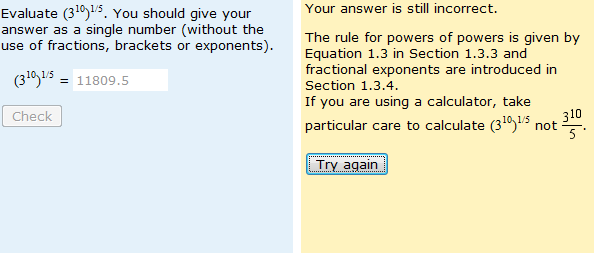
It was the analysis of question such as the one above that led to one of my early insights into mathematical misunderstandings. I discovered then that a common answer to this question was 11809.8. This is caused by students finding 310 and then dividing the whole thing by 5. So either students misunderstand the rules of precedence or they just can’t use their calculator. As you’ll see from above, I have since added targeted feedback in response to errors of this type.
A more recent analysis has shown that the most common error is now to calculate 3 x 10/5 (which gives an answer of 6). These students don’t really understand what powers are at all – it is like saying that 23 is the same as 2 x 3.
And there’s another common error, namely to find 3 x (1010)1/5 i.e. 3 x 102(which equals 300), demonstrating a confusion between powers and powers of 10 – or just using the wrong calculator button.
The correct answer, of course, is 9 (i.e. 32).
In addition to leading to additional insight into specific misunderstandings, this question demonstrates several principles of the whole approach. Firstly, although I have given the correct and incorrect answers as a series of options in the title of this blog post, it is a free text question. So students work out their own response rather than selecting one. I believe this gives more powerful evidence of the fact that these responses are the result of genuine misunderstandings (or careless calculator use) rather than being guesses. Of course, were I devising a mulitple-choice question now, I might use these as distractors – but I would not have thought of those particular options when the original question was written 10 years ago.
The fact that similar errors occur in different variants of the question also adds to the strength of the findings. Having said that, sometimes the fact that different variants behave differently can add insight too. In this case, the first error I have described (giving an answer of 11809.8) is less common in variants such as this one, than when the error results in a nice round number. It appears that students realise that an answer like 11809.8 is unlikely to be a correct solution – and so they double check.
Finally, note that what was once the most common incorrect response does not have that honour any more. I’d like to think that this is because of the targeted feedback that has been added. In addition, I am adding a screencast to Maths for Science in an attempt to resolve the other misunderstandings. When you begin to appreciate the common misunderstandings of your students, you can attempt to do something about them.