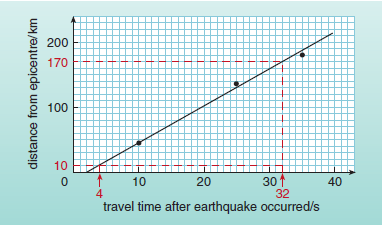
Working yesterday on the chapter on Graphs and Gradient for the new edition of Maths for Science, I remembered the other student error that I have seen in iCMA questions. When asked to find the gradient of a graph like the one shown below, some students essentially ‘count squares’.
In this case, they would give the rise (actually (170-10) km = 160 km) as 16, since that is how many squares there are vertically between the red lines. By counting squares horizontally, they would give the corresponding run as 28 (which is correct apart from the fact that the units – seconds in this case – have been omitted). So the gradient would be given as 0.57 instead of 5.7 km/s.
A related problem is students measuring the rise and run using a ruler, again rather than reading values from the axes. Perhaps we encourage both these behaviours by making an analogy between the gradient of a line and the gradient of a road. When finding the gradient of a road, we are concerned with actual lengths, not the representations of other things on a graph.