You are here
- Home
- Professor Ian Short
Professor Ian Short
Professional biography
I am Professor of Geometry and REF Lead for B10 Mathematical Sciences. I joined the Open University in 2010 having previously worked at the University of Cambridge and the National University of Ireland Maynooth. Before that I was a PhD student at the University of Cambridge.
Research interests
My research interests include geometry and dynamics, complex analysis, continued fractions, and group theory. Here are some recent projects.
Classifying SL2-tilings
This work describes a unifying approach to classifying SL2-tilings using the geometric, numeric, and combinatorial properties of the Farey graph. It is funded by the EPSRC grant EP/W002817/1 and is carried out in collaboration with postdoctoral researcher Matty Van-Son and research students Margaret Stanier and Andrei Zabalotskii. See https://arxiv.org/abs/1904.11900, published in the Transactions of the American Mathematical Society, 2023.
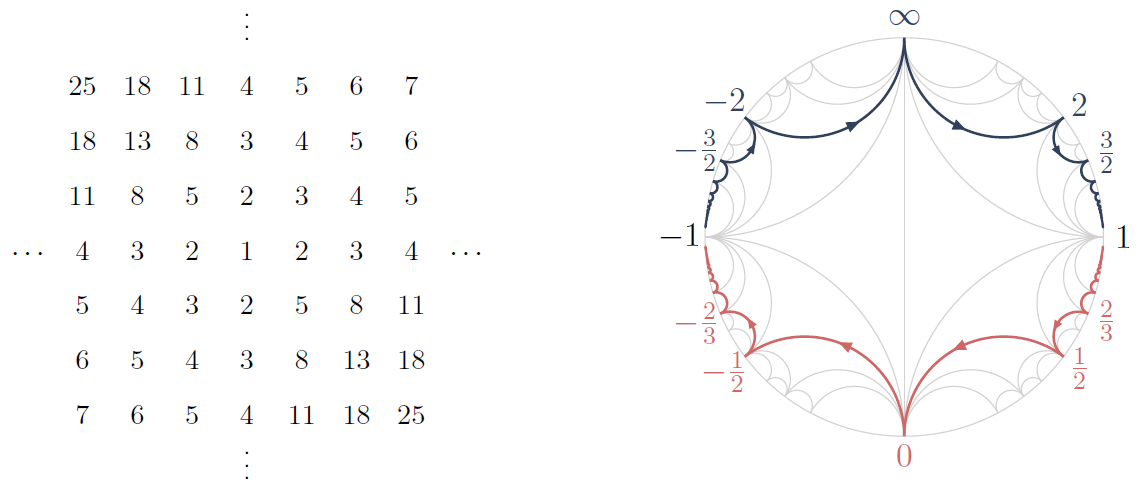
SL2-tiling and corresponding paths in the Farey graph
Semigroups of isometries of the hyperbolic plane
This project relates nonautonomous dynamical systems of hyperbolic isometries with semigroups of hyperbolic isometries, and develops the theory of such semigroups. See https://arxiv.org/abs/1609.00576 (joint with Matthew Jacques), published in International Mathematics Research Notices, 2022.
Forward and backward limit sets
Necessary and sufficient conditions for convergence of continued fractions
We describe a simple algorithm for determining whether an integer continued fraction converges, inspired by the geometry of the Farey complex. This is joint work with Margaret Stanier http://arxiv.org/abs/2102.10173, published in the Proceedings of the American Mathematical Society, 2022.

Homotopies in the Farey complex
Nilpotent covers of symmetric and alternating groups
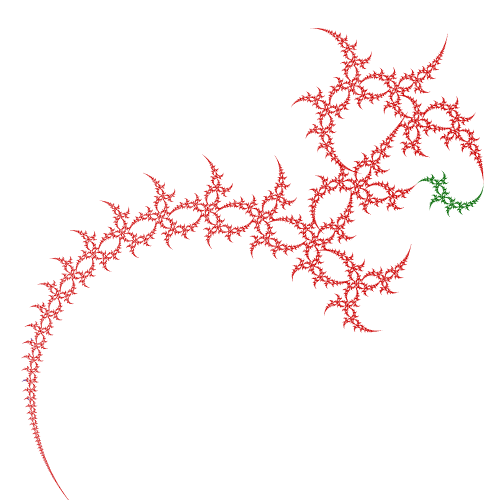
We prove that the symmetric group on n letters has a unique minimal cover by maximal normal subgroups. This cover has striking properties; for example, the number of conjugacy classes in the cover is equal to the number of partitions of n into distinct positive integers. This research was funded in part by a Mentoring African Researchers in Mathematics grant held jointly with Nick Gill and carried out in collaboration with PhD student Kimei Arphaxad Ngwava from Moi University, Keyna. The research https://arxiv.org/abs/2005.13869 is published in the Bulletin of the Belgian Mathematical Society – Simon Stevin, 2022.
Forward limit sets of substitution semigroups
We consider the dynamics of finitely-generated semigroups of substitutions of finite alphabets, which is closely related to the theory of S-adic substitutions. We examine the forward limit set of a semigroup; this is the collection of all S-adic limits with the same generating set. This is joint work with research student Ibai Aedo and our fine colleague Uwe Grimm, who died in 2021 during preparation of the paper.
First-letter graph for some substitutions
Teaching interests
I teach at all levels of the OU mathematics curriculum. I authored several chapters of the level 1 modules MST124 Essential mathematics 1 and MST125 Essential mathematics 2, I chaired the level 3 module M337 Complex analysis (2016–2021), and I chaired the MSc Mathematics module M829 Analytic number theory II (2012–2022). Additionally, I chaired production of the following modules.
M337 Complex analysis
I chaired the rewrite of M337, completed in 2018. The revised books for M337 have approximately 1150 pages, well over 1000 figures, and a wealth of exercises and solutions. Here are the four beautifully illustrated module texts and the module handbook:

M337 module texts
M840 Riemann surfaces
I chaired the M840 dissertation topic Riemann surfaces, released in 2021. This is a sequel to M337 for those students of the MSc Mathematics degree who might wish to pursue research in the field.
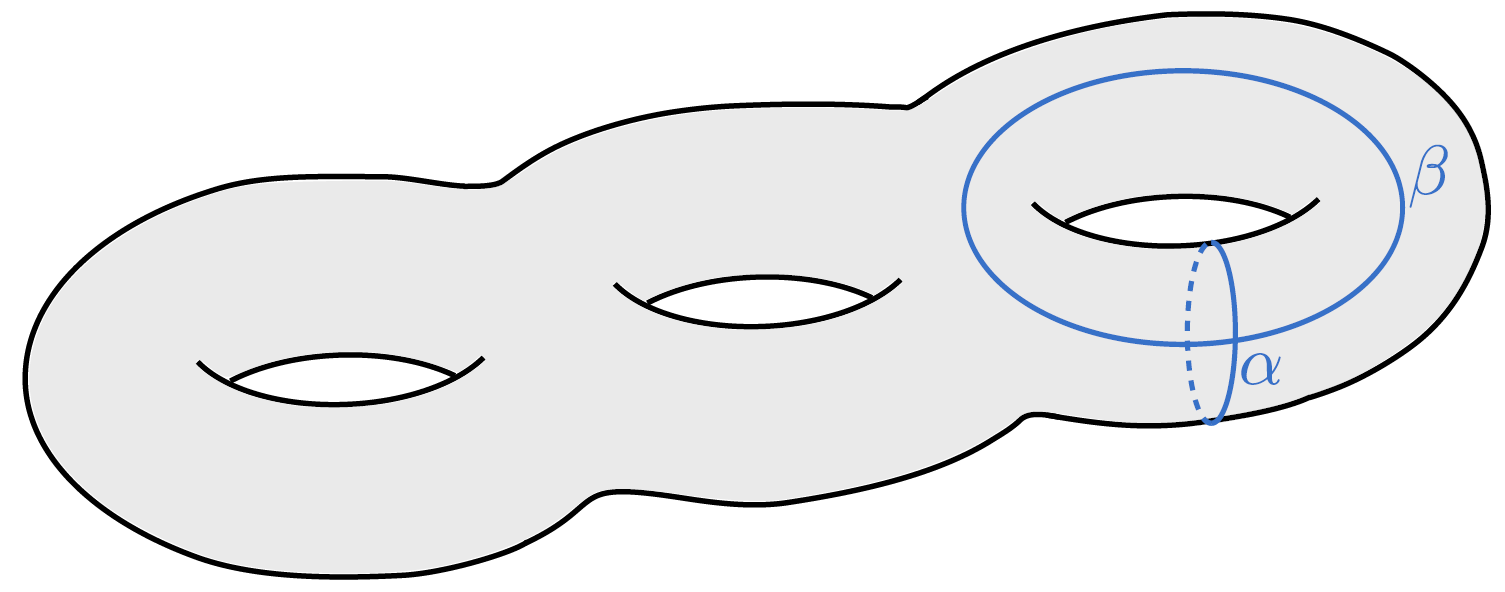
Closed curves on a compact Riemann surface of genus 3
M839 Differential geometry with applications
I am chairing production of a new MSc module M839 Differential geometry with applications, which is scheduled for first presentation in 2024. This module will develop the geometry of curves and surfaces. It will culminate in the Gauss–Bonnet theorem.
Impact and engagement
Aperiodic tilings – a meeting and mathematical art exhibition in honour of Uwe Grimm
In 2022 with Charlotte Webb and Reem Yassawi I organised the three-day event Aperiodic tilings, which brought together mathematicians, engineers, scientists, and artists to share research and communicate artwork in the subject of aperiodic tilings. The exhibition included painting, sculptures, 3D printing, musical art, computer-generated images, and hands-on activities. It was open to the public and attracted 750 visitors. An online gallery displays artwork from the event. The event celebrated the research and public engagement work of Uwe Grimm.












Artwork from Aperiodic tilings
Navigating by numbers
I lead the Navigating by numbers outreach programme. The purpose of the programme is to communicate an attractive network of geometric and numeric ideas centred around the Farey graph. This involves Coxeter's frieze patterns, SL2-tilings, continued fractions, dessins d'enfants, hyperbolic geometry, and a host of other mathematical concepts. This programme complements my EPSRC project EP/W002817/1 on SL2-tilings.
.png)
The Farey graph
Research groups
| Name | Type | Parent Unit |
|---|---|---|
| Pure Mathematics Research Group | Group | Faculty of Mathematics, Computing and Technology |
| Pure Maths: Analysis & Geometry Research Group | Group | Faculty of Mathematics, Computing and Technology |
Externally funded projects
The Farey framework for SL2-tilings
| Role | Start date | End date | Funding source |
|---|---|---|---|
| Lead | 01 Jul 2022 | 30 Jun 2025 | EPSRC Engineering and Physical Sciences Research Council |
This research programme will develop a geometric framework to bring together a significant body of work in the field of SL2-tilings and to answer major open questions in the field. The subject of this proposal originated in simple number patterns which thirty years after their discovery proved to be a small part of a profound mathematical theory. These number patterns were first studied in the 1970s and named friezes because of their repetitive appearance. Conway and Coxeter devised an attractive way to classify friezes using polygons divided into triangles - triangulated polygons. Independent of this, the powerful theory of cluster algebras was developed in the 2000s, which found deep applications in diverse mathematical fields. It was observed that friezes could be constructed from cluster algebras, and this led to the development of new number patterns, more general than friezes, called SL2-tilings. The field of SL2-tilings flourished in the decade since their inception, with leading groups in the UK at Leeds and Newcastle. Connections were uncovered to other mathematical fields, including algebraic combinatorics, difference equations, projective geometry, and representation theory. There has been significant focus on classifying types of SL2-tilings, usually with models inspired by Conway and Coxeter's triangulated polygons, to give mathematicians a visual way of interpreting SL2-tilings. In 2015, it was observed that Conway and Coxeter's theory can be explained elegantly using a geometric object called the Farey complex, which can be thought of loosely as an infinite triangulated polygon. It has a geometry associated to it known as hyperbolic geometry, the geometry of special relativity from physics. The PI took up the baton in 2020, using the Farey complex to offer a unified approach to a host of recent works on SL2-tilings with integer entries. This proposal advances this unifying work to offer geometric models for classes of SL2-tilings that have thus far resisted classification. To achieve this, we will apply techniques from hyperbolic geometry and the field of continued fractions, which is concerned with representing numbers; both are fields of expertise of the PI. There are three primary objectives, as follows. The first objective is to classify SL2-tilings modulo n, which are collections of SL2-tilings that use a type of arithmetic sometimes called clock arithmetic in which you add and subtract in the way you do on a clock. Until now no models have emerged for these SL2-tilings; they were something of a mystery. A highlight of the proposal will be the use of the little-known Farey complex of level n to model SL2-tilings of level n, just as the Farey complex models normal SL2-tilings. The second objective is to classify SL2-tilings with entries that are positive numbers, not necessarily integers. Here we must leave the Farey complex and instead use other tools from hyperbolic geometry, including chains of horocycles developed by the PI and Beardon in 2014. We will demonstrate that known models for classifying positive integer SL2-tilings are special cases of geometric models for more general positive real SL2-tilings. The third, most ambitious objective is to tackle the notoriously thorny class of wild integer SL2-tilings. First we will restrict our attention to those wild integer SL2-tilings with only finitely many zero entries. To approach these, we introduce bifurcating paths in the Farey complex, a new type of geometric object suitable to the task. We will then explore the extent to which bifurcating paths can be used to classify the full collection of wild integer SL2-tilings. The outcome of the project will be a framework which encompasses and advances a substantial body of cutting-edge research in SL2-tilings. Each of the three objectives introduces distinct, new techniques. The research will strengthen the UK's world-leading profile in this rapidly expanding field. | |||
Aperiodic tilings – a meeting and mathematical art exhibition in honour of Uwe Grimm
| Role | Start date | End date | Funding source |
|---|---|---|---|
| Lead | 01 Jun 2022 | 31 May 2023 | Heriot-Watt University (International Centre for Mathematical Sciences) |
: "Research meeting for the event Aperiodic tilings – a meeting and mathematical art exhibition in honour of Uwe Grimm". | |||
EPSRC Mathematical Sciences Research Associate Fund
| Role | Start date | End date | Funding source |
|---|---|---|---|
| Lead | 01 Oct 2021 | 30 Jun 2023 | EPSRC Engineering and Physical Sciences Research Council |
EPSRC Research Associates in Mathematical Sciences have offered £100,000 for research associate positions with the M&S department to start in October 2021. | |||
Lyapunov Exponents and Spectral Properties of Aperiodic Structures
| Role | Start date | End date | Funding source |
|---|---|---|---|
| Lead | 01 Apr 2019 | 31 Mar 2023 | EPSRC Engineering and Physical Sciences Research Council |
Characterising aperiodically ordered structures and understanding their properties has been a major area of activity since the discovery of quasicrystals in the 1980s. There are three types of spectral quantities which are commonly studied in this context: (1) the diffraction measure, which is the Fourier transform of the autocorrelation measure and is directly related to the outcome of diffraction experiments; (2) the dynamical spectrum, which is related to the action of translations on the system; (3) the Schroedinger spectrum, which is the energy spectrum of a (discrete) Schroedinger operator describing the motion of electrons in an aperiodic system. While a good understanding of the relationshop between diffraction and dynamical spectra has recently emerged, the relation between these two spectra and those of the corresponding (discrete) Schroedinger operator has remained elusive. This project aims at investigating this relationship, building on recent results that point to a key role played by Lyapunov exponents of matrix product cocycles for the diffraction spectrum. | |||
LMS Scheme 1 Grant
| Role | Start date | End date | Funding source |
|---|---|---|---|
| Lead | 01 Sep 2016 | 31 Aug 2017 | LMS London Mathematical Society |
A grant for £1700 from the London Mathematical Society to host the One Day Function Theory Meeting at De Morgan House, London, on 12 September 2016. | |||
Publications
Journal articles
Classifying SL2-tilings (2023)
Short, Ian
Transactions of the American Mathematical Society, 376 (pp. 1-38)
Forward limit sets of semigroups of substitutions (2023)
Aedo, Ibai; Grimm, Uwe and Short, Ian
arxiv/Forward limit sets of semigroups of substitutions ((Early access))
Nilpotent covers of symmetric and alternating groups (2022-12)
Gill, Nick; Kimeu, Ngwava and Short, Ian
Bulletin of the Belgian Mathematical Society – Simon Stevin, 29(2) (pp. 249-266)
Necessary and sufficient conditions for convergence of integer continued fractions (2022-02)
Short, Ian and Stanier, Margaret Rosemary
Proceedings of the American Mathematical Society, 150(2) (pp. 617-631)
Stability of the Denjoy–Wolff theorem (2021-06-21)
Christodoulou, Argyrios and Short, Ian
Annales Academiæ Scientiarum Fennicæ, 26 (pp. 421-431)
Semigroups of isometries of the hyperbolic plane (2021)
Jacques, Matthew and Short, Ian
International Mathematics Research Notices, 2022(9) (pp. 6403-6463)
Normal Families of Möbius Maps (2020-03-05)
Beardon, Alan; Minda, David and Short, Ian
Computational Methods and Function Theory, 20 (pp. 523-538)
Repeated compositions of Möbius transformations (2020)
Jacques, Matthew and Short, Ian
Ergodic Theory and Dynamical Systems, 40(2) (pp. 437-452)
Escaping sets of continuous functions (2019-03)
Short, Ian and Sixsmith, David J.
Journal d'Analyse Mathematique, 137(2) (pp. 875-869)
A hyperbolic-distance inequality for holomorphic maps (2019)
Short, Ian and Christodoulou, Argyrios
Annales Academiæ Scientiarum Fennicæ, Mathematica, 44 (pp. 293-300)
Substitution-based structures with absolutely continuous spectrum (2018-08-31)
Chan, Lax; Grimm, Uwe and Short, Ian
Indagationes Mathematicae, 29(4) (pp. 1072-1086)
Geodesic Rosen Continued Fractions (2016-12-30)
Short, Ian and Walker, Mairi
The Quarterly Journal of Mathematics, 67(4) (pp. 519-549)
The parabola theorem on continued fractions (2016-04-11)
Short, Ian
Computational Methods and Function Theory, 16(4) (pp. 653-675)
A geometric representation of continued fractions (2014-05)
Beardon, Alan F. and Short, Ian
American Mathematical Monthly, 121(5) (pp. 391-402)
Maximal buttonings of trees (2014)
Short, Ian
Discussiones Mathematicae Graph Theory, 34(2) (pp. 415-420)
On the product decomposition conjecture for finite simple groups (2013-11)
Gill, Nick; Pyber, László; Short, Ian and Szabó, Endre
Groups, Geometry, and Dynamics, 7(4) (pp. 867-882)
Conformal automorphisms of countably connected regions (2013-01-09)
Short, Ian
Conformal Geometry and Dynamics, 17 (pp. 1-5)
Conjugacy in Thompson's group $F$ (2013)
Short, Ian and Gill, Nick
Proceedings of the American Mathematical Society, 141 (pp. 1529-1538)
Hausdorff dimension of sets of divergence arising from continued fractions (2012-04)
Short, Ian
Proceedings of the American Mathematical Society, 140(4) (pp. 1371-1385)
Geodesic continued fractions (2012-03-08)
Beardon, A. F.; Hockman, M. and Short, I.
Michigan Mathematical Journal, 61(1) (pp. 133-150)
Flowability of plane homeomorphisms (2012)
O'Farrell, Anthony; Le Roux, Frédéric; Roginskaya, Maria and Short, Ian
Annales de l'Institut Fourier, 62(2) (pp. 619-639)
Visualizing uncertainty about the future (2011-09-09)
Spiegelhalter, David; Pearson, Mike and Short, Ian
Science, 333(6048) (pp. 1393-1400)
Rigidity of configurations of balls and points in the N-sphere (2011-06-29)
Crane, Edward and Short, Ian
The Quarterly Journal of Mathematics, 62(2) (pp. 351-362)
Ford circles, continued fractions, and rational approximation (2011-02)
Short, Ian
American Mathematical Monthly, 118(2) (pp. 130-135)
The Seidel, Stern, Stolz and Van Vleck Theorems on continued fractions (2010-06)
Beardon, Alan F. and Short, Ian
Bulletin of the London Mathematical Society, 42(3) (pp. 457-466)
Norms of Möbius maps (2010-06)
Beardon, Alan F. and Short, Ian
Bulletin of the London Mathematical Society, 422(3) (pp. 499-505)
Reversible maps and composites of involutions in groups of piecewise linear homeomorphisms of the real line (2010-03)
Gill, Nick and Short, Ian
Aequationes Mathematicae, 79(1-2) (pp. 23-37)
Reversibility in the group of homeomorphisms of the circle (2009-10)
Gill, Nick; O'Farrell, Anthony G. and Short, Ian
Bulletin of the London Mathematical Society, 41(5) (pp. 885-897)
Conjugacy Classification of Quaternionic Möbius Transformations (2009-04)
Parker, John R. and Short, Ian
Computational Methods and Function Theory, 9(1) (pp. 13-25)
Reversibility in the Diffeomorphism Group of the Real Line (2009)
O'Farrell, Anthony and Short, Ian
Publicacions Matemàtiques, 53(2) (pp. 401-405)
Reversible maps in isometry groups of spherical, Euclidean and hyperbolic space (2008-09-18)
Short, Ian
Mathematical Proceedings of the Royal Irish Academy, 108A(1) (pp. 33-46)
How much money do you need? (2008-01)
Short, Ian
Mathematical Spectrum, 40(2) (pp. 67-72)
Conical limit sets and continued fractions (2007-10-31)
Crane, Edward and Short, Ian
Conformal Geometry and Dynamics, 11 (pp. 224-249)
Conformal symmetries of regions (2007-07)
Beardon, Alan F. and Short, Ian
Irish Mathematical Society Bulletin, 59(1) (pp. 49-60)
Van Vleck's theorem on continued fractions (2007)
Beardon, Alan F. and Short, Ian
Computational Methods and Function Theory, 7(1) (pp. 185-203)
Reversible maps in the group of quaternionic Möbius transformations (2007)
Lávička, Roman; O'Farrell, Anthony G. and Short, Ian
Mathematical Proceedings of the Cambridge Philosophical Society, 143(1) (pp. 57-69)
Magic letter groups (2007)
Short, Ian and Pearson, Mike
Mathematical Gazette, 91(522) (pp. 493-499)
Hyperbolic geometry and the Hillam-Thron theorem (2006-04-07)
Short, Ian
Geometriae Dedicata, 119(1) (pp. 91-104)
The hyperbolic geometry of continued fractions K(1|bn) (2006)
Short, Ian
Annales Academiae Scientiarum Fennicae Mathematica, 31(2) (pp. 315-327)
A counterexample to a continued fraction conjecture (2006)
Short, Ian
Proceedings of the Edinburgh Mathematical Society. Series II, 49(3) (pp. 735-737)
Authored books
Reversibility in Dynamics and Group Theory (2015-05-31)
O'Farrell, Anthony G. and Short, Ian
London Mathematical Society Lecture Note Series
ISBN : 9781107442887 | Publisher : Cambridge University Press | Published : Cambridge
Conference items
Even-integer continued fractions and the Farey tree (2014)
Short, Ian and Walker, Mairi
In : SIGMAP 2014 (7 Jul 2014-11 July 2014, West Malvern, UK)
