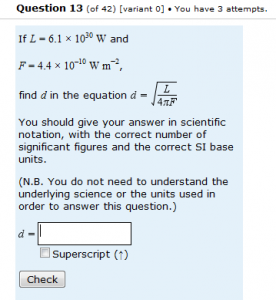
When I was doing the original analysis of student responses to Maths for Science assessment questions, I concentrated on questions that had been used summatively and also on questions that required students to input an answer rather than selecting a response. I reckoned that summative free-text questions would give me more reliable information on student misunderstandings than would be the case for formative-only and multiple-choice questions. Was this a valid assumption? I’ll start by considering student responses to a question that is similar to the one I have been discussing in the previous posts, but which is in use on the Maths for Science formative-only ‘Practice assessment’. The question is shown on the left. The Practice assessment is very heavily used and students can (and do) re-attempt questions as often as they would like to, being given different variants for extra practice.
The first thing to note is that, not surprisingly, this question is less well answered than its equivalents in the summative end-of-module assignments. Of 6732 uses, 1513 (22.5%) were correct at the first attempt, 1076 (16.0%) were correct at the second attempt and 527 (7.8%) were correct at the third attempt, leaving 3616 (53.7%) who didn’t get a completely correct answer, even after three attempts. It is also noteworthy (and common for non-trivial questions in formative-only uses of OpenMark) that there was a high percentage of blank responses and of responses that were repeated at second and third attempt without the correction of previous errors. After filtering out these responses, we were left with 13480 responses, of which 3116 (23.1%) were correct.
An analysis of the 100 most commonly given responses (a total set of 8054 responses) enables us to identify the following common themes:
Of the 8054 responses, 3111 (38.6%) were marked as correct.
A total of 1652 responses (20.5%) were numerically correct, but gave incorrect units. In more detail:
- There were 698 responses (8.7%) which were numerically correct but gave the units as m-2
- There were 571 responses (7.1%) which were numerically correct but gave the units as m2
- There were 205 responses (2.5%) which were numerically correct but gave the units as m-1
- There were 178 responses (2.2%) which were numerically correct but gave the units as W m-2
And what of other errors?:
- There were 1296 responses (16.1%) which were numerically correct but did not include any units.
- There were 435 responses (5.4%) where the student appeared to have rounded incorrectly.
- There were 324 responses (4.0%) where the student had calculated d2 rather than d, i.e. they had not taken the square root. One of the most pleasing things that I noticed was the fact that many of these people gave the units as m2 (which is of course consistent with their numerical answer).
- There were 234 responses (2.9%) which were numerically correct but who gave the answer to three significant figures (and quite a lot of those who gave three significant figures also omitted the units…).
So what can we conclude? The blank and repeated responses, and also the number of responses that have no units at all, gives some indication that students are not trying so hard on a purely formative assessment. Perhaps this means that we should have less confidence in the results of the analysis of errors, but I still think it has some useful things to tell us.
The fact that m-2 and m2 were the most common incorrect units suggests that students “forget” to take the square root of the units, or perhaps they think that the square root doesn’t apply to the units.
The fact that giving units of m-2 was the single most common mistake, and also that m-1 was on the list, suggests that students also have trouble seeing that the reciprocal of a negative power is a positive power. This is consistent with findings from other questions – students have problems with fractions, reciprocals and powers.