OpenMark e-assessment questions were used for the first time in a little 10-credit module called Maths for Science that has been running since 2002. I did some analysis years ago into the mistakes that students make, but I’m about to start writing a second edition of the module, so I’m revisiting this work. One of the things that amazed me when I first did the analysis and continues to amaze me now is that students are surprisingly good at rearranging equations. However, they are surprisingly bad at substituting values into equations to give a final result, complete with correct units and appropriate precision.
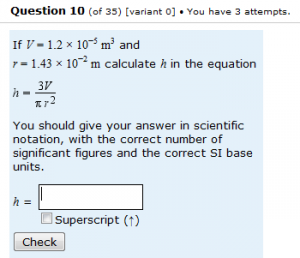 Consider the question illustrated on the left, which is in high-stakes summative use and which exists in a number of variants. For a combined data set of 1639 users of the question, 670 (40.9%) were correct at first attempt, 387 (23.6%) were correct at second attempt, 163 (9.9%) were correct at third attempt, and 419 (25.6%) were still not correct after three attempts. This resulted in a total of 3190 responses, of which just 1220 (38.2%) were completely correct.
Consider the question illustrated on the left, which is in high-stakes summative use and which exists in a number of variants. For a combined data set of 1639 users of the question, 670 (40.9%) were correct at first attempt, 387 (23.6%) were correct at second attempt, 163 (9.9%) were correct at third attempt, and 419 (25.6%) were still not correct after three attempts. This resulted in a total of 3190 responses, of which just 1220 (38.2%) were completely correct.
The most common problem, as you’ve probably guessed from the title of this post, was with the units. In general, it is not that people omit units entirely; units are given, but sadly they are wrong. The students are trying very hard, but clearly they struggle in this area. I’m struggling too – I fear that my teaching on this can’t be very good, but I don’t know what to do better. Students also have problems getting the number of significant figures correct.
The most common incorrect responses (for all variants of this question) were as follows:
- There were 205 responses (6.4% of all responses) which gave an otherwise correct answer with units of m2.
- There were 111 responses (3.5%) which gave correct units and a numerically correct answer, but expressed to three significant figures.
- There were 80 responses (2.5%) which gave a numerically correct value to two significant figures, but without any units. (Which could either be that they forgot the units, or thought that they cancelled out to give a dimensionless number.)
- There were 49 responses (1.5%) which gave an otherwise correct answer with units of m3.

Dear Sally,
What an interesting post again.
When reading it, I wondered if there are in fact problems with the set-up of the OpenMark system that disadvantages the student.
For example, I know from other systems that students must enter the required units in a separate box. This reinforces the fact that students must enter 2 separate answers and prevents that students make a probably unintended mistake. The advantage of this is also that a scoring algorithm can be used that acknowledges scores for the correct calculation as well as the correct units. The same counts for making mistakes with the correct number of significant figures. Making a mistake with that now results in a score of zero points whilst the student showed some understanding of the matter.
What do you think?
That’s a very interesting point Silvester.
For some questions I agree with you – and I certainly think it is is good to give partial credit and targeted feedback when a response is partly correct.
OpenMark can give separate entry boxes for different things – so if there is a fault it is mine as the designer of this particular question! I think we have sometimes been guilty of telling a student that their answer is incorrect when it is actually only incorrect in some ‘detail’. This is particularly unfortunate if we don’t give targeted feedback for the ‘detail’ (fortunately for this question we do – I’ll show this in another post).
However for this particular question (because of what it is assessing and where it comes in the Module) I want students to get used to writing a complete answer, without prompts from the system, so I don’t think I’d want multiple entry boxes. I think perhaps I ought to make this clearer in the question. I will also explore the possibility of giving partial credit if only one aspect is incorrect.
Many thanks
Sally
Pingback: e-assessment (f)or learning » Blog Archive » The case of units and variables