Investigating whether variants of a question are of equivalent difficulty

We have devised a range of tools to determine whether or not the variants of a question are of equivalent difficulty.

Statistics such as ‘facility index’ (mean score) and standard deviation are available separately for each variant of a question. These statistics can be useful, especially when used in conjunction with the tools described below. However on the basis of these statistics alone it is not possible to decide whether or not a difference in, for example, facility index is of statistical significance.
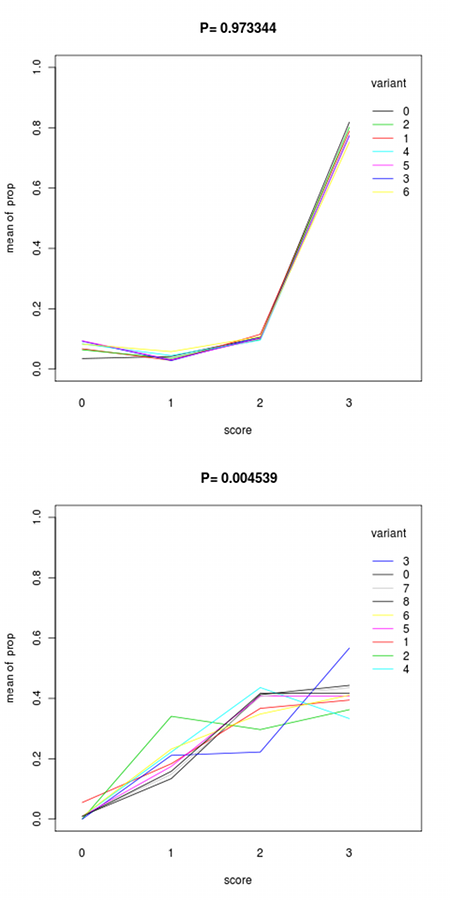
Plots showing the proportions of students scoring 0, 1, 2 or 3 for each variant (two examples are given below). These plots are useful because two variants of a question can have the same facility index even if they behave differently (for example, most students might get one variant of a question right at the second attempt whilst getting another variant right at either the first or third attempt).
A single figure (a probability p) that allows us to say with some certainty whether or not there is a real difference between variants. This figure tests the null hypothesis that the chance of scoring 0, 1, 2 or 3 is fixed across the variants. p is the probability that, under the null hypothesis that all variants are equal, the number of students achieving each score for each variant would be at least as extreme as in the actual data. If p<0.05 then you should reject the null hypothesis i.e. you can be reasonably sure that the different variants of this question are not of equivalent difficulty.

A picture paints a thousand words: The proportion of students scoring 0, 1, 2 or 3 for each variant of two iCMA questions.