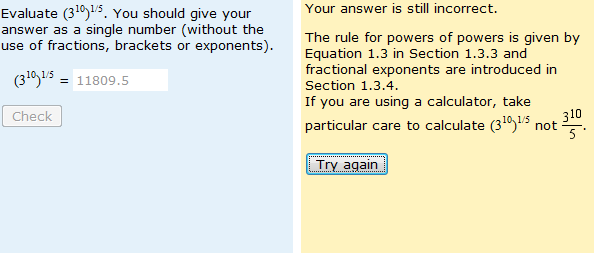
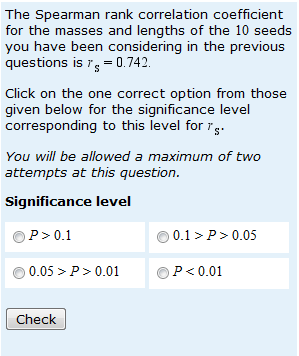
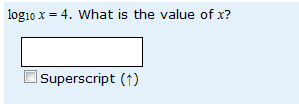
I attended another JISC ‘webinair’ yesterday. These provide a wonderful opportunity to keep up to date with developments in assessment for minimal outlay of time (one hour) and at no cost. Today’s webinair featured Gunter Saunders from the University of Westminster and Peter Chatterton from Daedelus eWorld Limited taking about the Making Assessment Count (MAC) Project.
The aims of the project include helping students to engage with the assessment process and using technology to help connect student reflections on assessment with their tutors. The technology in this case is E-reflect, which enables tutors to generate self-review questionnaires. Students complete these and get automated feedback. It’s all very simple multiple-choice stuff, but after receiving the feedback students write an entry in their learning journal and at this stage they enter into more meaningful dialogue with their tutor.
It took me a little while to work out what E-reflect is (and I’m still not sure I’ve got it right) but I’ve found a helpful website meant for University of Westmister staff and a Youtube channel (we were meant to watch one of these videos during the webinair, but I misunderstood the instruction and looked at the wrong one!).
I wonder if we could get something like this working at the OU? Just maybe. S154 Science starts here (the wonderful 10-credit module that I chair) is about to start its final presentation and the material will be re-used in the 30-credit S140 Introducing science. S154 uses a learning journal and I am determined to keep this aspect in S140 – but some students don’t like it. Definitely worth thinking about a slightly different approach.
Interestingly, given my previous post in which I explained one of the difficulties with teaching at a distance, duing the webinair I found myself pointing out that personalised support doesn’t have to be face-to-face. Dialogue can take place electronically! I’m sure we could run a system like E-reflect (probably using Moodle Quiz) in an entirely online environment to encourage reflection and as a starting point for dialogue. I just need to think about whether this would be a good way forward for S140.
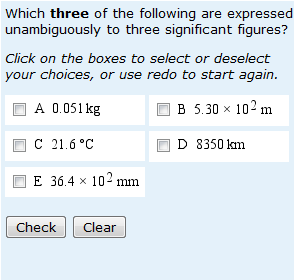 I’ve said before that students are not good at giving answers to an appropriate number of significant figures. But what do they do wrong? The question shown on the left provides some insight.
I’ve said before that students are not good at giving answers to an appropriate number of significant figures. But what do they do wrong? The question shown on the left provides some insight.